Question

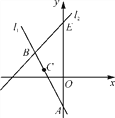
【題目】如圖，直線l1在平面直角坐標系中，直線l1與y軸交于點A，點B(－3，3)也在直線l1上，將點B先向右平移1個單位長度，再向下平移2個單位長度得到點C，點C恰好也在直線l1上．

(1)求點C的坐標和直線l1的解析式；

(2)已知直線l2：y＝x＋b經過點B，與y軸交于點E，求△ABE的面積.

Answer 1

【答案】(1)y＝－2x－3.(2) 13.5

【解析】（1）根據平移的性質得到點C的坐標；把點B、C的坐標代入直線方程y=kx+b（k≠0）來求該直線方程；

（2）根據點B的坐標求得直線l2的解析式，據此求得相關線段的長度，并利用三角形的面積公式進行解答．

解：(1)由題意得：點C的坐標為(－2，1)．

設直線l1的解析式為y＝kx＋c，

∵點B，C在直線l1上，

∴，

解得,

∴直線l1的解析式為y＝－2x－3.

(2)把點B的坐標代入y＝x＋b，

得3＝－3＋b，

解得b＝6，

∴y＝x＋6，

∴點E的坐標為(0，6)，

∵直線y＝－2x－3與y軸交于A點，

∴A的坐標為(0，－3)，

∴AE＝6＋3＝9，

∵B(－3，3)，

∴S△ABE＝×9×|－3|＝13.5.