
【題目】若點A(x1,1)、B(x2,﹣2)、C(x3,﹣3)在反比例函數(shù)y=﹣![]() 的圖象上,則x1、x2、x3的大小關(guān)系是( )
的圖象上,則x1、x2、x3的大小關(guān)系是( )
A.x1<x2<x3B.x1<x3<x2C.x3<x1<x2D.x2<x1<x3
科目:初中數(shù)學 來源: 題型:
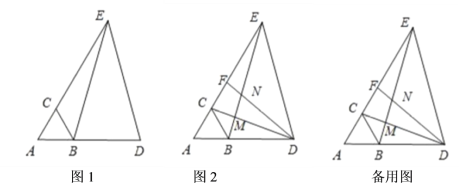
【題目】如圖,在等邊![]() 中,延長
中,延長![]() 至點
至點![]() ,延長
,延長![]() 交
交![]() 的中垂線于點
的中垂線于點![]() ,連接
,連接![]() ,
,![]() .
.
(1)如圖1,若![]() ,
,![]() ,求
,求![]() 的長;
的長;
(2)如圖2,連接![]() 交
交![]() 于點
于點![]() ,在
,在![]() 上取一點
上取一點![]() ,連接
,連接![]() 交
交![]() 于點
于點![]() ,且
,且![]() ,求證:
,求證:![]() ;
;
(3)在(2)的條件下,若![]() 直接寫出線段
直接寫出線段![]() ,
,![]() ,
,![]() 的等量關(guān)系
的等量關(guān)系
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】某校科技夏令營的學生在![]() 位老師的帶領(lǐng)下,準備赴北京大學參觀,體驗大學生活.現(xiàn)有兩家旅行社前來洽談,報價均為每人
位老師的帶領(lǐng)下,準備赴北京大學參觀,體驗大學生活.現(xiàn)有兩家旅行社前來洽談,報價均為每人![]() 元,且各有優(yōu)惠.希望旅行社表示:帶隊老師免費,學生按
元,且各有優(yōu)惠.希望旅行社表示:帶隊老師免費,學生按![]() 折收費;青春旅行社表示師生一律按
折收費;青春旅行社表示師生一律按![]() 折收費.經(jīng)核算發(fā)現(xiàn),參加兩家旅行社的實際費用正好相等.
折收費.經(jīng)核算發(fā)現(xiàn),參加兩家旅行社的實際費用正好相等.
(1)該校參加科技夏令營的學生共有多少人?
(2)如果又增加了部分學生,學校應(yīng)選擇哪家旅行社?為什么?
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,在平面直角坐標系xOy中,菱形ABCD的對角線AC與BD交于點P(-1,2),AB⊥x軸于點E,正比例函數(shù)y=mx的圖像與反比例函數(shù)![]() 的圖像交于A,P兩點.
的圖像交于A,P兩點.
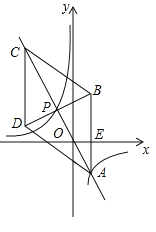
(1)求m,n的值與點A的坐標
(2)求![]() 的值
的值
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】某事業(yè)單位組織全體職工參加了“抗擊疫情,服務(wù)社會”的活動為了了解單位職工參加活動情況,從單位職工中隨機抽取部分職工進行調(diào)查,統(tǒng)計了該天他們打掃街道、去敬老院服務(wù)和社區(qū)文藝演出的人數(shù),并繪制了如下不完整的條形統(tǒng)計圖和扇形統(tǒng)計圖,請根據(jù)兩幅統(tǒng)計圖中的信息,回答下列問題:
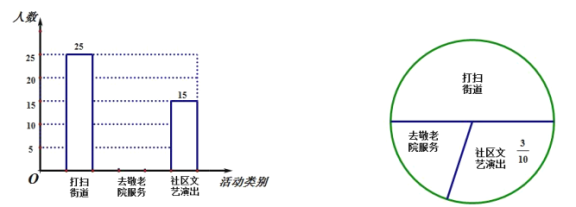
![]() 本次抽樣調(diào)查共抽取了多少名單位職工?
本次抽樣調(diào)查共抽取了多少名單位職工?
![]() 通過計算補全條形統(tǒng)計圖;
通過計算補全條形統(tǒng)計圖;
![]() 若該事業(yè)單位共有
若該事業(yè)單位共有![]() 名職工,請你估計該單位去敬老院的職工有多少名.
名職工,請你估計該單位去敬老院的職工有多少名.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】按要求作圖,不要求寫作法,但要保留作圖痕跡.
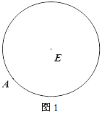
(1)如圖1,A為圓E上一點,請用直尺(不帶刻度)和圓規(guī)作出圓內(nèi)接正方形;
(2)我們知道,三角形具有性質(zhì),三邊的垂直平分線相交于同一點,三條角平分線相交于一點,三條中線相交于一點,事實上,三角形還具有性質(zhì):三條高交于同一點,請運用上述性質(zhì),只用直尺(不帶刻度)作圖:
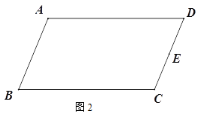
①如圖2,在□ABCD中,E為CD的中點,作BC的中點F;
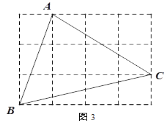
②圖3,在由小正方形組成的網(wǎng)格中,的頂點都在小正方形的頂點上,作△ABC的高AH
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】為了弘揚傳統(tǒng)文化,提高學生文明意識,育才學校組織全校80個班級進行"誦經(jīng)典,傳文明"表演賽,比賽后對各班成績進行了整理,分成4個小組(![]() 表示成績,單位:分),并根據(jù)成績設(shè)立了特等獎、一等獎、二等獎和三等獎.
表示成績,單位:分),并根據(jù)成績設(shè)立了特等獎、一等獎、二等獎和三等獎.![]() 組(三等獎):
組(三等獎):![]() ;
;![]() 組(二等獎):
組(二等獎):![]() ;
;![]() 組(一等獎):
組(一等獎):![]() ;
;![]() 組(特等獎):
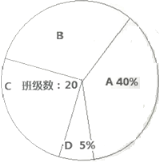
組(特等獎):![]() .并繪制如下不完整的扇形統(tǒng)計圖.
.并繪制如下不完整的扇形統(tǒng)計圖.
請根據(jù)圖中信息,解答下列問題:
(1)求扇形統(tǒng)計圖中,![]() 組對應(yīng)的圓心角是多少度?
組對應(yīng)的圓心角是多少度?
(2)學校從獲得特等獎的班級中選取了2名男生和2名女生組成代表隊參加了區(qū)級比賽,由于表現(xiàn)突出,被要求再從這4名學生中隨機選取兩名同學參加市級比賽,請用列表或畫樹狀圖的方法,求恰好選中一名男生和一名女生的概率.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】在一條道路上,甲從A地出發(fā)到B地,乙從B地出發(fā)到A地,乙的速度是80千米/小時,兩人同時出發(fā)各自到達終點后停止,設(shè)行駛過程中甲、乙之間的距離為s千米,甲行駛的時間為t小時,s與t之間的函數(shù)關(guān)系如圖所示,則下列說法錯誤的是( )
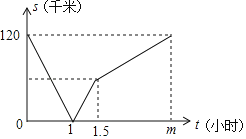
A.乙出發(fā)1小時與甲在途中相遇
B.甲從A地到達B地需行駛3小時
C.甲在1.5小時后放慢速度行駛
D.乙到達A地時甲離B地還有60干米
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,AB是一垂直于水平面的建筑物,某同學從建筑物底端B出發(fā),先沿水平方向向右行走20米到達點C,再經(jīng)過一段坡度(或坡比)為i=1:0.75、坡長為10米的斜坡CD到達點D,然后再沿水平方向向右行走40米到達點E(A,B,C,D,E均在同一平面內(nèi)).在E處測得建筑物頂端A的仰角為24°,則建筑物AB的高度約為(參考數(shù)據(jù):sin24°≈0.41,cos24°≈0.91,tan24°=0.45)( )

A. 21.7米 B. 22.4米 C. 27.4米 D. 28.8米
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com