
【題目】已知![]() 是關于
是關于![]() 的二次多項式,且二次項系數和一次項系數分別為
的二次多項式,且二次項系數和一次項系數分別為![]() 和
和![]() ,在數軸上
,在數軸上![]() 、
、![]() 、
、![]() 三點所對應的數分別是
三點所對應的數分別是![]() 、
、![]() 、
、![]() .
.
![]()
(1)有一動點![]() 從點
從點![]() 出發,以每秒
出發,以每秒![]() 個單位的速度向左運動,多少秒后,
個單位的速度向左運動,多少秒后,![]() 到
到![]() 、
、![]() 、
、![]() 的距離和為
的距離和為![]() 個單位?
個單位?
(2)在(1)的條件下,當點![]() 移動到點
移動到點![]() 時立即掉頭,速度不變,同時點
時立即掉頭,速度不變,同時點![]() 和點
和點![]() 分別從點
分別從點![]() 和點
和點![]() 出發,向右運動,點
出發,向右運動,點![]() 的速度
的速度![]() 個單位
個單位![]() 秒,點
秒,點![]() 的速度
的速度![]() 個單位
個單位![]() 秒.設點
秒.設點![]() 、
、![]() 、
、![]() 所對應的數分別是
所對應的數分別是![]() 、
、![]() 、
、![]() ,點
,點![]() 出發的時間為
出發的時間為![]() ,當
,當![]() 時,求
時,求![]() 的值.
的值.
【答案】(1)2秒;(2)8t-26
【解析】
(1)先根據題意求出a、b、c的值,再根據圖形得到:![]() 到
到![]() 、
、![]() 、
、![]() 的距離和為
的距離和為![]() 個單位,則此時P一定在B和原點之間,設點P表示的數為x,列出方程,解方程,從而求得時間;
個單位,則此時P一定在B和原點之間,設點P表示的數為x,列出方程,解方程,從而求得時間;
(2)先求出點P追上點M的時間為![]() 秒,點N追上點M的時間為
秒,點N追上點M的時間為![]() ,點N追上點P的時間為
,點N追上點P的時間為![]() ,由此畫出對應的圖形,再利用絕對值的性質求解.
,由此畫出對應的圖形,再利用絕對值的性質求解.
(1)因為![]() 是關于
是關于![]() 的二次多項式,且二次項系數和一次項系數分別為
的二次多項式,且二次項系數和一次項系數分別為![]() 和
和![]() ,
,
所以a=10,b=6,c=-3,
當點P在A、B兩點之間時,不可能存在點![]() 到
到![]() 、
、![]() 、
、![]() 的距離和為
的距離和為![]() 個單位;
個單位;
當點P在點C和原點之間時,不可能存在點![]() 到
到![]() 、
、![]() 、
、![]() 的距離和為
的距離和為![]() 個單位;
個單位;
當點P在點B和原點之間時,設P點表示的數為x,則:
x+3+(6-x)+(10-x)=15
解得x=4,
所以AP=10-4=6,
所以點P運動的時間為![]() 秒;
秒;
(2)因為點P追上點M的時間為![]() 秒,點N追上點M的時間為
秒,點N追上點M的時間為![]() ,點N追上點P的時間為
,點N追上點P的時間為![]() ,且
,且![]() ,
,
所以此時點對應的M、N、P的位置如圖所示,對應的數為![]() =3t+6、
=3t+6、![]() =t+10、
=t+10、![]() =5t-3
=5t-3
![]()
∴![]()
=3t+6-(t+10)+(5t-3)-(t+10)-[(3t+6)-(5t-3)]
=3t+6-t-10+5t-3-t-10-3t-6+5t-3
=8t-26.


科目:初中數學 來源: 題型:
【題目】綜合與實踐
數學活動課上,小紅畫了如圖1所示的兩個共用直角頂點的等腰直角三角形![]() 與等腰直角三角形
與等腰直角三角形![]() ,其中
,其中![]() ,
,![]() ,連接
,連接![]() ,
,![]() 、
、![]() 、
、![]() 分別為邊
分別為邊![]() 、
、![]() 、
、![]() 的中點,連接
的中點,連接![]() 、
、![]() .
.
操作發現:
小紅發現了:![]() 、
、![]() 有一定的關系,數量關系為_____________________________;位置關系為_________________.
有一定的關系,數量關系為_____________________________;位置關系為_________________.

類比思考:
如圖2,在圖1的基礎上,將等腰直角三角形![]() 繞點
繞點![]() 旋轉一定的角度,其它條件都不變,小紅發現的結論還成立嗎?請說明理由.(提示:連接
旋轉一定的角度,其它條件都不變,小紅發現的結論還成立嗎?請說明理由.(提示:連接![]() 、
、![]() 并延長交于一點
并延長交于一點![]() )
)
深入探究:
在上述類比思考的基礎上,小紅做了進一步的探究.如圖3,作任意一個三角形![]() ,其中
,其中![]() ,在三角形外側以
,在三角形外側以![]() 為腰作等腰直角三角形
為腰作等腰直角三角形![]() ,以
,以![]() 為腰作等腰直角三角形
為腰作等腰直角三角形![]() ,分別取斜邊
,分別取斜邊![]() 、
、![]() 與邊
與邊![]() 的中點
的中點![]() 、
、![]() 、
、![]() ,連接
,連接![]() 、
、![]() 、
、![]() ,試判斷三角形
,試判斷三角形![]() 的形狀,并說明理由.
的形狀,并說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了提升城市容貌,規范城市管理.我區城管某巡邏車在一條東西方向的公路上巡邏,規定向東為正,向西為負.某天,汽車從出發點開始所走的路程分別為:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() (單位:千米).隊長要求匯報位置.
(單位:千米).隊長要求匯報位置.
(1)此時,駕駛員如何向隊長描述他的位置?
(2)如果隊長命令他馬上返回到出發點,這次巡邏(從出發點開始到最后又返回出發點)共耗油多少升?(已知每千米耗油![]() 升)
升)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,平行四邊形ABCD,DE⊥AB.垂足E在BA的延長線上,BF⊥DC,垂足F在DC的延長線上.

(1)求證:四邊形BEDF是矩形;
(2)如圖2,若M、N分別為AD、BC的中點,連接EM、EN、FM、FN,求證:四邊形EMFN是平行四邊形.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】數學興趣小組研究某型號冷柜溫度的變化情況,發現該冷柜的工作過程是:
當溫度達到設定溫度﹣20℃時,制冷停止,此后冷柜中的溫度開始逐漸上升,當上升到﹣4℃時,制冷開始,溫度開始逐漸下降,當冷柜自動制冷至一20℃時,制冷再次停止,..
按照以上方式循環進行
同學們記錄了44min 內15個時間點冷柜中的溫度y(℃) 隨時間x(min) 的變化情況,制成下表:
時間x/min | … | 4 | 8 | 10 | 16 | 20 | 21 | 22 | 23 | 24 | 28 | 30 | 36 | 40 | 42 | 44 | … |
溫度y/℃ | … | ﹣20 | ﹣10 | ﹣8 | ﹣5 | ﹣4 | ﹣8 | ﹣12 | ﹣16 | ﹣20 | ﹣10 | ﹣8 | ﹣5 | ﹣4 | a | ﹣20 | … |
(1)通過分析發現,冷柜中的溫度y是時間x的函數.
①當4≤x<20時,寫出一個符合表中數據的函數解析式 ;
②當20≤x<24時,寫出一個符合表中數據的函數解析式 ;
(2)溫度不低于﹣8℃的持續時間為 min;
(3)A的值為 .
查看答案和解析>>
科目:初中數學 來源: 題型:
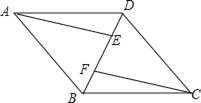
【題目】已知:如圖,四邊形ABCD是平行四邊形,AE∥CF,且分別交對角線BD于點E,F.
(1)求證:△AEB≌△CFD;
(2)連接AF,CE,若∠AFE=∠CFE,求證:四邊形AFCE是菱形.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知點P是![]() 對角線BD上的一點,分別過點B、D作AP的垂線,垂足分別為點E、F,
對角線BD上的一點,分別過點B、D作AP的垂線,垂足分別為點E、F,
(1)如圖1,若點P為BD中點,∠BAP=30°,AD=5,CD=8,求AF的長;
(2)如圖2,若點E在CD上,BE=DE,延長DF至G,使DG=AB,點H在BD上,連接AH、GH、EH、FH,若∠G=∠BAH,求證:HE=HF.


查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】把球放在長方體紙盒內,球的一部分露出盒外,其截面如圖所示,已知EF=CD=4 cm,則球的半徑長是( )

A. 2cm B. 2.5cm C. 3cm D. 4cm
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】把下列一元二次方程化成一般式,并寫出方程中的各項及各項的系數.
(1)![]() ;
;
一般式:_________________.
二次項為____,二次項系數為____,一次項為____,
一次項系數為____,常數項為____.
(2)![]() ;
;
一般式:_________________.
二次項為____,二次項系數為____,一次項為____,
一次項系數為____,常數項為____.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com