
【題目】四邊形ABCD是正方形(提示:正方形四邊相等,四個角都是90°)

(1)如圖1,點G是BC邊上任意一點(不與點B、C重合),連接AG,作BF⊥AG于點F,DE⊥AG于點E.
求證:△ABF≌△DAE;
(2)直接寫出(1)中,線段EF與AF、BF的等量關系 ;
(3)①如圖2,若點G是CD邊上任意一點(不與點C、D重合),連接AG,作BF⊥AG于點F,DE⊥AG于點E,則圖中全等三角形是 ,線段EF與AF、BF的等量關系是 ;
②如圖3,若點G是CD延長線上任意一點,連接AG,作BF⊥AG于點F,DE⊥AG于點E,線段EF與AF、BF的等量關系是 ;
(4)若點G是BC延長線上任意一點,連接AG,作BF⊥AG于點F,DE⊥AG于點E,請畫圖、探究線段EF與AF、BF的等量關系.
【答案】(1)證明見解析;(2)EF=AF-BF;(3)①△ABF≌△DAE;EF=BF-AF;②EF=AF+BF;(2)EF=BF-AF.
【解析】試題分析:(1)根據正方形性質得出AB=AD,∠DAB=90°,根據垂直定義得出∠AED=∠AFB=90°,根據等角的余角相等求出∠ADE=∠BAF,根據AAS證出兩三角形全等即可;
(2)根據全等得出AE=BF,代入即可求出答案;
(3)①△ABF≌△DAE,EF=BF-AF,證法與(1)(2)類似;②EF=AF+BF,證明過程類似;
(4)根據正方形性質得出AB=AD,∠DAB=90°,根據垂直定義得出∠AED=∠AFB=90°,求出∠ADE=∠BAF,根據AAS證出兩三角形全等即可.
試題解析:
(1)證明:∵四邊形ABCD是正方形,
∴AB=AD,∠DAB=90°,
∴∠DAE+∠BAE=90°,
∵DE⊥AG,BF⊥AG,
∴∠AED=∠AFB=90°,
∴∠EAD+∠ADE=90°,
∴∠ADE=∠BAF,
∵在△ABF和△DAE中
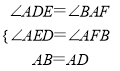 ,
,
∴△ABF≌△DAE(AAS);
(2)解:線段EF與AF、BF的等量關系是EF=AF-BF,
理由是:∵由(1)知:△ABF≌△DAE,
∴BF=AE,
∴EF=AF-AE=AF-BF,
故答案為:EF=AF-BF;
(3)①解:△ABF≌△DAE,EF=BF-AF,
理由是:∵四邊形ABCD是正方形,
∴AB=AD,∠DAB=90°,
∴∠DAE+∠BAE=90°,
∵DE⊥AG,BF⊥AG,
∴∠AED=∠AFB=90°,
∴∠EAD+∠ADE=90°,
∴∠ADE=∠BAF,
∵在△ABF和△DAE中
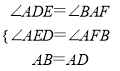
∴△ABF≌△DAE(AAS);
∴AE=BF,
∴EF=AE-AF=BF-AF,
故答案為:△ABF≌△DAE,EF=BF-AF;
②解:EF=AF+BF,
理由是:∵四邊形ABCD是正方形,
∴AB=AD,∠DAB=90°,
∴∠DAE+∠BAF=180°-90°=90°,
∵DE⊥AG,BF⊥AG,
∴∠AED=∠AFB=90°,
∴∠EAD+∠ADE=90°,
∴∠ADE=∠BAF,
∵在△ABF和△DAE中
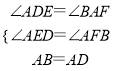 ,
,
∴△ABF≌△DAE(AAS);
∴AE=BF,
∴EF=AE+AF=AF+BF,
故答案為:EF=AF+BF;
(4)解: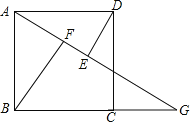
與以上證法類似:△ABF≌△DAE(AAS);
∴AE=BF,
∴EF=AE-AF=BF-AF;
即EF=BF-AF.


科目:初中數學 來源: 題型:
【題目】某廠生產A,B兩種產品,其單價隨市場變化而做相應調整,營銷人員根據前三次單價變化的情況,繪制了如下統計表及不完整的折線圖:

并求得了A產品三次單價的平均數和方差:
![]() ;
; ![]()
(1)補全圖中B產品單價變化的折線圖,B產品第三次的單價比上一次的單價降低了 %;
(2)求B產品三次單價的平均數和方差,并比較哪種產品的單價波動小;
(3)該廠決定第四次調價,A產品的單價仍為6.5元/件,若B產品第四次調價后為m元(3<m<4),此時B產品四次單價的中位數是A產品這四次單價的中位數的![]() 倍,求m.
倍,求m.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在每個小正方形的邊長均為1個單位長度的方格紙中,有一個[Math Processing Error] ![]()
![]() 和一點O,[Math Processing Error]
和一點O,[Math Processing Error] ![]()
![]() 的頂點與點O均與小正方形的頂點重合。
的頂點與點O均與小正方形的頂點重合。

(1)在方格紙中,將[Math Processing Error] ![]()
![]() 向下平移6個單位長度得到[Math Processing Error]
向下平移6個單位長度得到[Math Processing Error] ![]()
![]() ,請畫[Math Processing Error]
,請畫[Math Processing Error] ![]()
![]() .
.
(2)在方格紙中,將[Math Processing Error] ![]()
![]() 繞點O旋轉180°得到[Math Processing Error]
繞點O旋轉180°得到[Math Processing Error] ![]()
![]() ,請畫[Math Processing Error]
,請畫[Math Processing Error] ![]()
![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com