【題目】如圖，△ABC三個頂點的坐標分別為A（1，1）、B（4，2）、C（3，4）．
(1)請畫出△ABC向左平移5個單位長度后得到的△A1B1C1；
(2)請畫出△ABC關于x軸對稱的△A2B2C2三個頂點A2、B2、C2的坐標；
(3)在x軸上求作一點P，使△PAB的周長最小，請畫出△PAB，并直接寫出P的坐標．
閱讀快車系列答案科目：初中數學 來源： 題型：
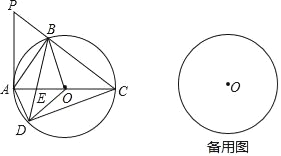
【題目】如圖，在△ABC中，∠ABC=90°，⊙O是△ABC外接圓，點D是圓上一點，點D、B分別在AC兩側，且BD=BC，連接AD、BD、OD、CD，延長CB到點P，使∠APB=∠DCB．
（1）求證：AP為⊙O的切線；
（2）若⊙O的半徑為1，當△OED是直角三角形時，求△ABC的面積；
（3）若△BOE、△DOE、△AED的面積分別為a、b、c，試探究a、b、c之間的等量關系式，并說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】隨著人們環保意識的增強，越來越多的人選擇低碳出行，各種品牌的山地自行車相繼投放市場.順風車行五月份
型車的銷售總利潤為
元，
型車的銷售總利潤為
元.且型車的銷售數量是型車的
倍，已知銷售型車比型車每輛可多獲利
元.
（1）求每輛型車和型車的銷售利潤；
（2）若該車行計劃一次購進
兩種型號的自行車共
臺且全部售出，其中型車的進貨數量不超過型車的倍，則該車行購進型車、型車各多少輛，才能使銷售總利潤最大？最大銷售總利潤是多少？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖1，在Rt△ABC中，∠C=90°，AC=6，BC=8，動點P從點A開始沿邊AC向點C以1個單位長度的速度運動，動點Q從點C開始沿邊CB向點B以每秒2個單位長度的速度運動，過點P作PD∥BC，交AB于點D，連接PQ分別從點A、C同時出發，當其中一點到達端點時，另一點也隨之停止運動，設運動時間為t秒（t≥0）．
（1）直接用含t的代數式分別表示：QB= ，PD= ．
（2）是否存在t的值，使四邊形PDBQ為菱形？若存在，求出t的值；若不存在，說明理由．并探究如何改變Q的速度（勻速運動），使四邊形PDBQ在某一時刻為菱形，求點Q的速度；
（3）如圖2，在整個運動過程中，求出線段PQ中點M所經過的路徑長．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，已知反比例函數y=
（x＞0）與正比例函數y=x（x≥0）的圖象，點A（1，5）、點A′（5，b）與點B′均在反比例函數的圖象上，點B在直線y=x上，四邊形AA′B′B是平行四邊形，則B點的坐標為_____．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知四邊形ABCD是菱形，AB=4，∠ABC=60°，∠EAF的兩邊分別與射線CB，DC相交于點E，F，且∠EAF=60°．
（1）如圖1，當點E是線段CB的中點時，直接寫出線段AE，EF，AF之間的數量關系；
（2）如圖2，當點E是線段CB上任意一點時（點E不與B、C重合），求證：BE=CF；
（3）如圖3，當點E在線段CB的延長線上，且∠EAB=15°時，求點F到BC的距離．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知A(n，-2)，B(1，4)是一次函數y=kx+b的圖象和反比例函數y=
的圖象的兩個交點，直線AB與y軸交于點C．
(1)求反比例函數和一次函數的關系式；
(2)求△AOC的面積；
(3)求不等式kx+b-<0的解集(直接寫出答案)．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在平面直角坐標系中，已知
，
兩點，且
、
滿足
，點
是射線
上的動點（不與
，
重合），將線段
平移到
，使點與點
對應，點
與點
對應，連接
，
.
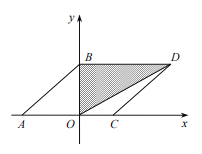
（1）求出點和點的坐標；
（2）設三角形
面積為
，若
，求
的取值范圍；
（3）設
，
，
，請給出
，
，
滿足的數量關系式，并說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
