【題目】（閱讀材料）平面直角坐標系中，點P（x，y）的橫坐標x的絕對值表示為|x|，縱坐標y的絕對值表示為|y|，我們把點P（x，y）的橫坐標與縱坐標的絕對值之和叫做點P（x，y）的勾股值，記為[P]，即[P]=|x|+|y|（其中的“+”是四則運算中的加法），例如點P（1，2）的勾股值[P]=|1|+|2|=3．
（1）求點A（
, 
）的勾股值[A]，
（2）若將點A向上平移3個單位，再向左平移2個單位后得到點B，請直接寫出點B的坐標，并求出點B的勾股值 [B]；
（3）若點M在x軸的上方，其橫，縱坐標均為整數，且[M]=3，請直接寫出點M的坐標．
科目：初中數學 來源： 題型：
【題目】如圖，在△ABC中，AB=AC，D是邊BC上一點，DE⊥AB，DF⊥AC，垂足分別是E,F，△AEF∽△ABC．
（1）求證：△AED≌△AFD；
（2）若BC=2AD，求證：四邊形AEDF是正方形．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，將Rt△ABC繞直角頂點B逆時針旋轉90°得到△DBE，DE的延長線恰好經過AC的中點F，連接AD，CE．
（1）求證：AE＝CE；
（2）若BC＝
，求AB的長．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在平面直角坐標系中，菱形ABCD在第一象限內，邊BC與x軸平行，A，B兩點的縱坐標分別為3，1，反比例函數y= 
的圖象經過A，B兩點，則菱形ABCD的面積為（ ）
A.2
B.4
C.2 
D.4
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，AB∥CD，CF平分∠ECD，HC⊥CF交直線AB于H，AG平分∠HAE交HC于G，EJ∥AG交CF于J，∠AEC＝80°，則下列結論正確的有（ ）個．
①∠BAE+∠ECD＝80°；②CG平分∠ICE；③∠AGC＝140°；④∠EJC﹣∠AGH＝90°．
A.1B.2C.3D.4
查看答案和解析>>
科目：初中數學 來源： 題型：
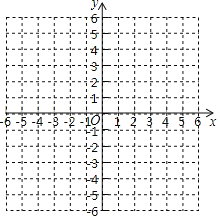
【題目】如圖，已知平面直角坐標系中，A點坐標為（﹣4，4），B（﹣4，0）C（1，3），解答下列各題：
（1）按題中所給坐標在圖中畫出△ABC并直接寫出△ABC的面積；
（2）畫出△ABC先向右平移5個單位長度再向下平移3個單位長度的△A'B'C'，并直接寫出A'，B′，C'的坐標；
（3）直接寫出△ABC按照（2）問要求平移到△A'B'C'的過程中，△ABC所掃過的圖形的面積．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】（1）如圖1，在四邊形
中，
，
、
分別是
、
的中點，連接
并延長，分別與
、
的延長線交于點
、
，證明：
．
請將證明的過程填寫完整：
證明：連接
，取的中點
，連接
、
．
是的中點，是的中點，
________，
_______，同理：
_______，
_______，
，
，
又
，
，
，
．
（2）運用上題方法解決下列問題：
問題一：如圖2，在四邊形
中，
與相交于點
，，、分別是、的中點，連接，分別交
、于點、，請判斷
的形狀，并說明理由；
問題二：如圖3，在鈍角
中，
，
點在
上，、分別是、的中點，連接并延長，與的延長線交于點
，連接
，若
，
是直角三角形且
，求證：．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在△ABC 中，點 D 是邊 BC 上的點（與 B、C 兩點不重合），過點 D作 DE∥AC，DF∥AB，分別交 AB、AC 于 E、F 兩點，下列說法正確的是（ ）
A. 若 AD 平分∠BAC，則四邊形 AEDF 是菱形
B. 若 BD＝CD，則四邊形 AEDF 是菱形
C. 若 AD 垂直平分 BC，則四邊形 AEDF 是矩形
D. 若 AD⊥BC，則四邊形 AEDF 是矩形
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
