
【題目】王老師從本校九年級質量檢測的成績中隨機地抽取一些同學的數學成績做質量分析,他先按照等級繪制這些人數學成績的扇形統計圖,如圖(1)所示,數學成績等級標準見表1,又按分數段繪制成績分布表,如表2,
表1
等級 | 分數x的范圍 |
A | a≤x≤100 |
B | 80≤x<a |
C | 60≤x<80 |
D | 0≤x<60 |
表2
分數段 | x<60 | 60≤x<70 | 70≤x<80 | 80≤x<90 | 90≤x≤100 |
人數 | 5 | 10 | m | 12 | n |
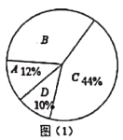
分數段為90≤x≤100的n個人中,其成績的中位數是95分.
根據以上信息回答下面問題:
(1)王老師抽查了多少人?m、n的值分別是多少;
(2)小明在此考試中得了95分,他說自己在這些考試中數學成績是A等級,他說的對嗎?為什么?
(3)若此次測試數學學科普高的預測線是70分,該校九年級有900名學生,求數學學科達到普高預測線的學生約有多少人?
【答案】(1)m=12,n=11;(2)對的,理由見解析;(3)該校數學學科達到普高預測線的學生約有630人.
【解析】
(1)根據小于60的人數和所占的百分比求出總人數,再用總人數乘以小于80的人數所占的百分比求出小于80的人數,再減去小于70的人數,求出m,再用總人數減去小于90 的人數,求出n即可;
(2)先求出A等級的人數,再根據在分數段為90≤x≤100的人數和中位數的定義即可推斷出小明說的對不對;
(3)用總人數乘以數學學科普高的預測線的人數所占的百分比即可.
解:(1)王老師抽查的人數是:5÷10%=50(人),
小于80的人數有:50×(44%+10%)=27(人),
m=27-5-10=12(人),
n=50-5-10-12-12=11(人)
(2)對的,理由是:
∵分數段在![]() 的有11人,
的有11人,
∴這11個分數從大到小的順序排列后,第6個分數就是這組數據的中位數,即第6個數據是95,
∵等級![]() 所占抽查的百分比是12%,
所占抽查的百分比是12%,
∴等級![]() 的人數為
的人數為![]() (人),
(人),
∴![]() ,
,
∴小明這次測試的數學成績是![]() 等級是對的.
等級是對的.
(3)抽查的學生數學分數在70分及以上有![]() 人,占抽查人數的百分率為:
人,占抽查人數的百分率為:
![]() ,
,
∴該校數學學科達到普高預測線的學生約有![]() (人)
(人)


 中考解讀考點精練系列答案
中考解讀考點精練系列答案科目:初中數學 來源: 題型:
【題目】九年級某班準備選拔四名男生參加學校運動會接力比賽,進行了一次50米短跑測驗,成績如下,(單位:秒)6.9 7.0 7.1 7.2 7.0 7.4 7.3 7.5 7.0 7.4 7.3 6.8 7.0 7.1 7.3 6.9 7.1 7.2 7.4 6.9 7.0 7.2 7.0 7.2 7.6
班主任老師按0.2秒的組距分段,統計每個成績段出現的頻數,填入頻數分布表,并繪制了頻數分布直方圖.
成績段(秒) |
|
|
|
|
|
頻數 | 4 | 9 | 7 |
| 1 |
頻率 |
| 0.36 | 0.28 | 0.16 | 0.04 |
(1)求a、b值,并將頻數分布直方圖補充完整;
(2)請計算這次短跑測驗的優秀率(7.0秒及7.0秒以下);
(3)成績前四名的A、B、C、D同學組成九年級某班4×100米接力隊,其中成績最好的A同學安排在最后一棒(第4棒),另外三位同學隨機編排在其余三個棒次,畫樹狀圖或列表說明B、C兩位同學為相鄰棒次的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】母親節前夕,某花店準備采購一批康乃馨和萱草花,已知購買![]() 束康乃馨和
束康乃馨和![]() 束萱草花共需
束萱草花共需![]() 元;購買
元;購買![]() 束康乃馨和
束康乃馨和![]() 束萱草花共需
束萱草花共需![]() 元.
元.
(1)求康乃馨和萱草花的單價分別為多少元;
(2)經協商,購買康乃馨超過![]() 束時,每增加
束時,每增加![]() 束,單價降低
束,單價降低![]() 元;當超過
元;當超過![]() 束時,均按購買
束時,均按購買![]() 束時的單價購進,萱草花一律按原價購買.
束時的單價購進,萱草花一律按原價購買.
①購買康乃馨![]() 束時,康乃馨的單價為_______元;購買康乃馨
束時,康乃馨的單價為_______元;購買康乃馨![]() 束時,康乃馨的單價為_______元(用含
束時,康乃馨的單價為_______元(用含![]() 的代數式表示);
的代數式表示);
②該花店計劃購進康乃馨和萱草花共![]() 束,其中康乃馨超過
束,其中康乃馨超過![]() 束,且不超過
束,且不超過![]() 束,當購買康乃馨多少束時,購買兩種花的總金額最少,最少為多少元?
束,當購買康乃馨多少束時,購買兩種花的總金額最少,最少為多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
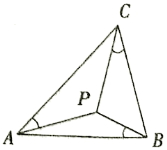
【題目】如圖,若![]() 內一點
內一點![]() 滿足
滿足![]() ,則點
,則點![]() 為
為![]() 的布洛卡點,三角形的布洛卡點由法國數學家和數學教育家克洛爾于1816年首次發現,但他的發現并未被當時的人們所注意.1875年,布洛卡點被一個數學愛好者法國軍官布洛卡重新發現,并用他的名字命名.問題:已知等腰直角三角形
的布洛卡點,三角形的布洛卡點由法國數學家和數學教育家克洛爾于1816年首次發現,但他的發現并未被當時的人們所注意.1875年,布洛卡點被一個數學愛好者法國軍官布洛卡重新發現,并用他的名字命名.問題:已知等腰直角三角形![]() 中,
中,![]() .若
.若![]() 為
為![]() 的布洛卡點,
的布洛卡點,![]() ,則
,則![]() 的值為( )
的值為( )
A.10B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
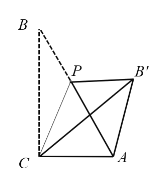
【題目】已知,Rt△ABC中,∠ACB=90°,∠B=30°,AC=1,點P是AB上一點,連接CP,將∠B沿CP折疊,使點B落在B'處.以下結論正確的有________
①當AB'⊥AC時,AB'的長為![]() ;
;
②當點P位于AB中點時,四邊形ACPB'為菱形;
③當∠B'PA=30°時,![]() ;
;
④當CP⊥AB時,AP:AB':BP=1:2:3.
查看答案和解析>>
科目:初中數學 來源: 題型:
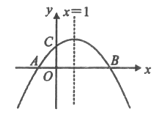
【題目】如圖,已知二次函數![]() 的圖象與x軸交于A,B兩點,與y軸交于點C,
的圖象與x軸交于A,B兩點,與y軸交于點C,![]() ,對稱軸為直線
,對稱軸為直線![]() ,則下列結論:①
,則下列結論:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() 是關于x的一元二次方程
是關于x的一元二次方程![]() 的一個根,其中正確的有_________個
的一個根,其中正確的有_________個
查看答案和解析>>
科目:初中數學 來源: 題型:
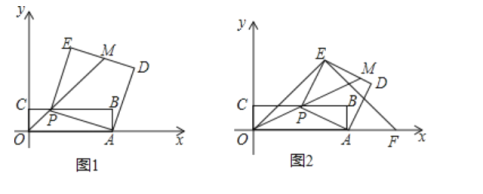
【題目】已知:如圖1,矩形OABC的兩個頂點A,C分別在x軸,y軸上,點B的坐標是(8,2),點P是邊BC上的一個動點,連接AP,以AP為一邊朝點B方向作正方形PADE,連接OP并延長與DE交于點M,設![]() .
.
(1)請用含a的代數式表示點P,E的坐標.
(2)如圖2,連接OE,并把OE繞點E逆時針方向旋轉90°得EF.若點F恰好落在x軸的正半軸上,求a與![]() 的值.
的值.
(3)如圖1,若點M為DE的中點,并且![]() ,點
,點![]() 在OP的延長線上,求
在OP的延長線上,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】萬州三中初中數學組深知人生最具好奇心和幻想力、創造力的時期是中學時代,經研究,為我校每一個初中生推薦一本中學生素質數育必讀書《數學的奧秘》,這本書就是專門為好奇的中學生準備的.這本書不但給于我們知識,解答生活中的疑惑,更重要的是培養我們細致觀察、認真思考、勤于動手的能力.經過一學期的閱讀和學習,為了了解學生閱讀效果,我們從初一、初二的學生中隨機各選20名,對《數學的奧秘》此書閱讀效果做測試(此次測試滿分:100分).通過測試,我們收集到20名學生得分的數據如下:
初一 | 96 | 100 | 89 | 95 | 62 | 75 | 93 | 86 | 86 | 93 |
95 | 95 | 88 | 94 | 95 | 68 | 92 | 80 | 78 | 90 | |
初二 | 100 | 98 | 96 | 95 | 94 | 92 | 92 | 92 | 92 | 92 |
86 | 84 | 83 | 82 | 78 | 78 | 74 | 64 | 60 | 92 |
通過整理,兩組數據的平均數、中位數、眾數和方差如表:
年級 | 平均數 | 中位數 | 眾數 | 方差 |
初一 | 87.5 | 91 | m | 96.15 |
初二 | 86.2 | n | 92 | 113.06 |
某同學將初一學生得分按分數段(![]() ,
,![]() ,
,![]() ,
,![]() ),繪制成頻數分布直方圖,初二同學得分繪制成扇形統計圖,如圖(均不完整),初一學生得分頻數分布直方圖 初二學生得分扇形統計圖(注:x表示學生分數)
),繪制成頻數分布直方圖,初二同學得分繪制成扇形統計圖,如圖(均不完整),初一學生得分頻數分布直方圖 初二學生得分扇形統計圖(注:x表示學生分數)
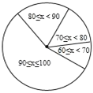
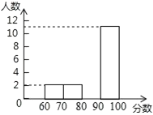
請完成下列問題:
(1)初一學生得分的眾數![]() ________;初二學生得分的中位數
________;初二學生得分的中位數![]() ________;
________;
(2)補全頻數分布直方圖;扇形統計圖中,![]() 所對用的圓心角為________度;
所對用的圓心角為________度;
(3)經過分析________學生得分相對穩定(填“初一”或“初二”);
(4)你認為哪個年級閱讀效果更好,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在四邊形ABCD中,AB//DC,∠A=60°,AD=DC=BC=4,點E沿A→D→C→B運動,同時點F沿A→B→C運動,運動速度均為每秒1個單位,當兩點相遇時,運動停止.則△AEF的面積y與運動時間x秒之間的圖象大致為( )
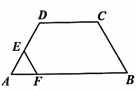
A.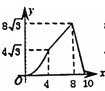 B.
B.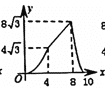 C.
C.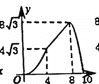 D.
D.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com