已知在平面直角坐標系xOy中,二次函數y=-2x2+bx+c的圖象經過點A(-3,0)和點B(0,6).
(1)求此二次函數的解析式;
(2)將這個二次函數的圖象向右平移5個單位后的頂點設為C,直線BC與x軸相交于點D,求∠ABD的正弦值;
(3)在第(2)小題的條件下,聯結OC,試探究直線AB與OC的位置關系,并說明理由.
解:(1)由題意得,

,
解得
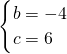
,
所以,此二次函數的解析式為y=-2x
2-4x+6;
(2)∵y=-2x
2-4x+6=-2(x+1)
2+8,
∴函數y=2x
2-4x+6的頂點坐標為(-1,8),
∴向右平移5個單位的后的頂點C(4,8),
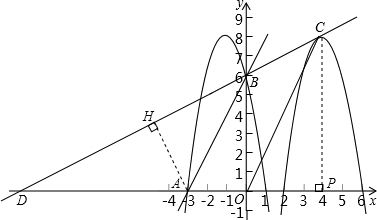
設直線BC的解析式為y=kx+b(k≠0),
則
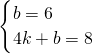
,
解得

,
所以,直線BC的解析式為y=

x+6,
令y=0,則

x+6=0,
解得x=-12,
∴點D的坐標為(-12,0),
過點A作AH⊥BD于H,
OD=12,BD=
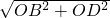
=
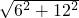
=6

,
AD=-3-(-12)=-3+12=9,
∵∠ADH=∠BDO,∠AHD=∠BOD=90°,
∴△ADH∽△BDO,
∴
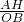
=
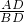
,
即
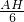
=
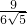
,
解得AH=

,
∵AB=

=
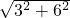
=3

,
∴sin∠ABD=
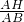
=
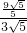
=

;
(3)AB∥OC.
理由如下:方法一:∵BD=6

,BC=
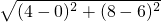
=2

,AD=9,AO=3,
∴

=
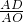
=3,
∴AB∥OC;
方法二:過點C作CP⊥x軸于P,
由題意得,CP=8,PO=4,AO=3,BO=6,
∴tan∠COP=
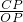
=
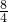
=2,
tan∠BAO=

=
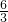
=2,
∴tan∠COP=tan∠BAO,
∴∠BAO=∠COP,
∴AB∥OC.
分析:(1)把點A、B的坐標代入函數解析式計算求出b、c的值,即可得解;
(2)先求出拋物線的頂點坐標,再根據向右平移橫坐標加,求出點C的坐標,設直線BC的解析式為y=kx+b(k≠0),然后利用待定系數法求出直線BC的解析式,再求出與x軸的交點D的坐標,過點A作AH⊥BD于H,先求出OD,再利用勾股定理列式求出BD,然后求出△ADH和△BDO相似,利用相似三角形對應邊成比例列式求出AH,再利用勾股定理,然后根據銳角的正弦等于對邊比斜邊列式計算即可得解;
(3)方法一:求出

=
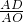
,然后根據平行線分線段成比例定理解答;
方法二:過點C作CP⊥x軸于P,分別求出∠BAO和∠COP的正切值,根據正切值相等求出∠BAO=∠COP,再根據同位角相等,兩直線平行解答.
點評:本題是二次函數綜合題,主要利用了待定系數法求二次函數解析式,待定系數法求一次函數解析式,銳角三角函數,相似三角形的判定與性質,作輔助線構造出相似三角形是解題的關鍵,作出圖形更形象直觀.

 ,
,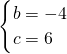 ,
,
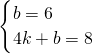 ,
, ,
, x+6,
x+6, x+6=0,
x+6=0,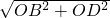 =
=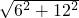 =6
=6 ,
,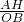 =
=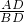 ,
,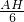 =
=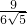 ,
, ,
, =
=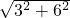 =3
=3 ,
,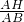 =
=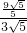 =
= ;
; ,BC=
,BC=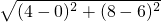 =2
=2 ,AD=9,AO=3,
,AD=9,AO=3, =
=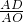 =3,
=3,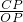 =
=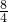 =2,
=2, =
=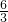 =2,
=2, =
=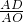 ,然后根據平行線分線段成比例定理解答;
,然后根據平行線分線段成比例定理解答;

 芒果教輔達標測試卷系列答案
芒果教輔達標測試卷系列答案 已知在平面直角坐標系xOy中,⊙O的半徑為1.
已知在平面直角坐標系xOy中,⊙O的半徑為1.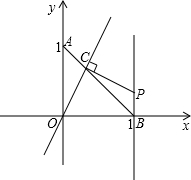 直線交線段AB于點C,過點C作OC的垂線與直線x=1相交于點P,設AC=t,點P的坐標為(1,y),
直線交線段AB于點C,過點C作OC的垂線與直線x=1相交于點P,設AC=t,點P的坐標為(1,y), 如圖,已知在平面直角坐標系中,平行四邊形ABCD頂點A(0,0),C(10,4),直線y=ax-2a-1將平行四邊形ABCD分成面積相等的兩部分,求a的值.
如圖,已知在平面直角坐標系中,平行四邊形ABCD頂點A(0,0),C(10,4),直線y=ax-2a-1將平行四邊形ABCD分成面積相等的兩部分,求a的值.