
【題目】如圖1,在平面直角坐標系中,拋物線y=![]() 與x軸交于A、B兩點(點A在點B的左側),與y軸交于點C,拋物線的頂點為點D,過點B作BC的垂線,交對稱軸于點E.
與x軸交于A、B兩點(點A在點B的左側),與y軸交于點C,拋物線的頂點為點D,過點B作BC的垂線,交對稱軸于點E.

(1)求證:點E與點D關于x軸對稱;
(2)點P為第四象限內的拋物線上的一動點,當△PAE的面積最大時,在對稱軸上找一點M,在y軸上找一點N,使得OM+MN+NP最小,求此時點M的坐標及OM+MN+NP的最小值;
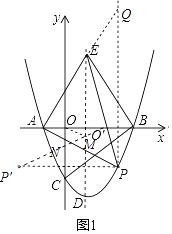
(3)如圖2,平移拋物線,使拋物線的頂點D在射線AD上移動,點D平移后的對應點為D′,點A的對應點A′,設拋物線的對稱軸與x軸交于點F,將△FBC沿BC翻折,使點F落在點F′處,在平面內找一點G,若以F′、G、D′、A′為頂點的四邊形為菱形,求平移的距離.
【答案】(1)證明見解析;(2)![]() ;(3)
;(3)![]() ,
, ![]() ,
, ![]()
【解析】試題分析:(1)首先求出A、B、C、D的坐標,再根據(jù)△EFB∽△BOC對應邊成比例得出方程,推出EF的長度,求出點E的坐標即可解決問題;
(2)過點P作PQ∥y軸,交直線AE于點Q.構建 二次函數(shù),利用二次函數(shù)的性質求出點P的坐標,作點O關于對稱軸的對稱點O′,作點P關于Y軸的對稱點P′,連接O′P′,分別交對稱軸、y軸于點M、N,此時M、N即為所求;
(3)由題意得F,A,D三點的坐標,設平移距離為![]() t,則得出A′,D′的坐標,可得A′F2,D′F′2,,A′D′2的長度,然后分三種情形:①當A′F2=D′F′2時,②當A′F′2=A′D′2時,③當D′F′2=A′D′2時列出方程即可解決問題.
t,則得出A′,D′的坐標,可得A′F2,D′F′2,,A′D′2的長度,然后分三種情形:①當A′F2=D′F′2時,②當A′F′2=A′D′2時,③當D′F′2=A′D′2時列出方程即可解決問題.
試題解析:解:(1)如圖1中,令y=0,得到![]() x2﹣
x2﹣![]() x﹣3=0,解得x=﹣
x﹣3=0,解得x=﹣![]() 或3
或3![]() ,∴A(﹣
,∴A(﹣ ![]() ,0),B(3
,0),B(3 ![]() ,0).
,0).
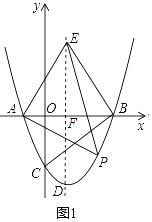
令x=0,可得y=﹣3,∴C(0,﹣3).
∵y= ![]() x2﹣
x2﹣ ![]() x﹣3=
x﹣3=![]() (x﹣
(x﹣ ![]() )2﹣4,∴頂點D(
)2﹣4,∴頂點D( ![]() ,﹣4),設對稱軸與x軸交于F,則BF=2
,﹣4),設對稱軸與x軸交于F,則BF=2 ![]() .
.
∵△EFB∽△BOC,∴ EF:OB=BF:OC,∴ ![]() ,∴EF=4,∴E(
,∴EF=4,∴E( ![]() ,4),∴E、D關于x軸對稱;
,4),∴E、D關于x軸對稱;
(2)過點P作PQ∥y軸,交直線AE于點Q.
∵yAE= ![]() x+2,∴設P(a,
x+2,∴設P(a, ![]() a2﹣
a2﹣![]() a﹣3),Q(a,
a﹣3),Q(a, ![]() a+2),(0<a<3
a+2),(0<a<3![]() ),∴PQ=(
),∴PQ=(![]() a+2)﹣(
a+2)﹣(![]() a2﹣
a2﹣![]() a﹣3)=﹣
a﹣3)=﹣![]() a2+2
a2+2 ![]() a+5,∴S△PAE=
a+5,∴S△PAE= ![]() PQ|xE﹣xA|=
PQ|xE﹣xA|= ![]() (﹣
(﹣![]() a2+2
a2+2![]() a+5)2
a+5)2![]() =﹣
=﹣![]() a2+4a+5
a2+4a+5![]() ,∴當a=
,∴當a=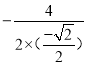 =2
=2![]() 時,S△PAE最大,此時P(2
時,S△PAE最大,此時P(2![]() ,﹣3).
,﹣3).
作點O關于對稱軸的對稱點O′(2![]() ,0),作點P關于Y軸的對稱點P′(﹣2
,0),作點P關于Y軸的對稱點P′(﹣2![]() ,﹣3).連接O′P′,分別交對稱軸、y軸于點M、N,此時M、N即為所求.
,﹣3).連接O′P′,分別交對稱軸、y軸于點M、N,此時M、N即為所求.
∴yP′O′=![]() x﹣
x﹣![]() ,當x=
,當x=![]() 時,y=﹣
時,y=﹣![]() ,∴M(
,∴M(![]() ,﹣
,﹣![]() ),∴OM+MN+NP的最小值O′P′=
),∴OM+MN+NP的最小值O′P′=![]() =
= ![]() ;
;
(3)∵F′(![]() ,﹣
,﹣![]() ),A(﹣
),A(﹣![]() +
+![]() t,﹣2t),D(
t,﹣2t),D(![]() ,﹣4),
,﹣4),
設平移距離為 ![]() t,則A′(﹣
t,則A′(﹣ ![]() +
+ ![]() t,﹣2t),D′(
t,﹣2t),D′( ![]() +
+![]() t,﹣4﹣2t),
t,﹣4﹣2t),
A′F2=6t2﹣24t+![]() ,D′F′2=6t2+
,D′F′2=6t2+![]() ,A′D′2=24,
,A′D′2=24,
①當A′F2=D′F′2時,6t2﹣24t+ ![]() =6t2+
=6t2+![]() ,解得t=1.
,解得t=1.
②當A′F′2=A′D′2時,6t2﹣24t+ ![]() =24,解得t=
=24,解得t=![]() .
.
③當D′F′2=A′D′2時,24=6t2+ ![]() ,解得t=
,解得t=![]() 或﹣
或﹣![]() (舍棄),
(舍棄),
∴平移的距離![]() t=
t= ![]() ,
, ![]() ,
, ![]() .
.


 暑假作業(yè)暑假快樂練西安出版社系列答案
暑假作業(yè)暑假快樂練西安出版社系列答案 新活力總動員暑系列答案
新活力總動員暑系列答案 龍人圖書快樂假期暑假作業(yè)鄭州大學出版社系列答案
龍人圖書快樂假期暑假作業(yè)鄭州大學出版社系列答案科目:初中數(shù)學 來源: 題型:
【題目】![]() 朗讀者
朗讀者![]() 自開播以來,以其厚重的文化底蘊和感人的人文情懷,感動了數(shù)以億計的觀眾,岳池縣某中學開展“朗讀”比賽活動,九年級
自開播以來,以其厚重的文化底蘊和感人的人文情懷,感動了數(shù)以億計的觀眾,岳池縣某中學開展“朗讀”比賽活動,九年級![]() 、
、![]() 班根據(jù)初賽成績,各選出5名選手參加復賽,兩個班各選出的5名選手的復賽成績
班根據(jù)初賽成績,各選出5名選手參加復賽,兩個班各選出的5名選手的復賽成績![]() 滿分為100分
滿分為100分![]() 如圖所示.
如圖所示.
平均數(shù) | 中位數(shù) | 眾數(shù) | |
九 | 85 | 85 | |
九 | 80 |
![]() 根據(jù)圖示填寫表格;
根據(jù)圖示填寫表格;
![]() 結合兩班復賽成績的平均數(shù)和中位數(shù),分析哪個班級的復賽成績較好;
結合兩班復賽成績的平均數(shù)和中位數(shù),分析哪個班級的復賽成績較好;
![]() 如果規(guī)定成績較穩(wěn)定班級勝出,你認為哪個班級能勝出?說明理由.
如果規(guī)定成績較穩(wěn)定班級勝出,你認為哪個班級能勝出?說明理由.

查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,菱形ABCD中,AB=4,E,F分別是AB、BC的中點,P是AC上一動點,則PF+PE的最小值是( )

A. 3B. ![]() C. 4D.
C. 4D. ![]()
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】某班“數(shù)學興趣小組”對函數(shù)y=|x|-2的圖象特征進行了探究,探究過程如下:
⑴自變量x的取值范圍是全體實數(shù),x與y的幾組對應值如下:
x | … | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | … |
y | … | 1 | m | -1 | -2 | n | 0 | 1 | 2 | … |
其中,m= ,n= .
⑵根據(jù)表中數(shù)據(jù),在如圖所示的平面直角坐標系中描點,并畫出函數(shù)圖象;

⑶觀察函數(shù)圖象,寫出一條特征: .
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,在Rt△ABC中,∠C=90°,∠ABC=30°,AB=8,將△ABC沿CB向右平移得到△DEF.若四邊形ABED的面積等于12,則平移距離等于( )

A.2 B.3 C.4 D.8
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖1,在平面直角坐標系中,直線AB與y軸交于點![]() ,與x軸交于點B,
,與x軸交于點B,![]() ,直線CD與y軸交于點D,與x軸交于點
,直線CD與y軸交于點D,與x軸交于點![]() ,
,![]() ,直線AB與直線CD交于點Q,E為直線CD上一動點,過點E作x軸的垂線,交直線AB于點M,交x軸于點N,連接AE、BE.
,直線AB與直線CD交于點Q,E為直線CD上一動點,過點E作x軸的垂線,交直線AB于點M,交x軸于點N,連接AE、BE.
![]() 求直線AB、CD的解析式及點Q的坐標;
求直線AB、CD的解析式及點Q的坐標;
![]() 當E點運動到Q點的右側,且
當E點運動到Q點的右側,且![]() 的面積為
的面積為![]() 時,在y軸上有一動點P,直線AB上有一動點R,當
時,在y軸上有一動點P,直線AB上有一動點R,當![]() 的周長最小時,求點P的坐標及
的周長最小時,求點P的坐標及![]() 周長的最小值.
周長的最小值.
![]() 在
在![]() 問的條件下,如圖2將
問的條件下,如圖2將![]() 繞著點B逆時針旋轉
繞著點B逆時針旋轉![]() 得到
得到![]() ,使點M與點G重合,點N與點H重合,再將
,使點M與點G重合,點N與點H重合,再將![]() 沿著直線AB平移,記平移中的
沿著直線AB平移,記平移中的![]() 為
為![]() ,在平移過程中,設直線
,在平移過程中,設直線![]() 與x軸交于點F,是否存在這樣的點F,使得
與x軸交于點F,是否存在這樣的點F,使得![]() 為等腰三角形?若存在,求出此時點F的坐標;若不存在,說明理由
為等腰三角形?若存在,求出此時點F的坐標;若不存在,說明理由
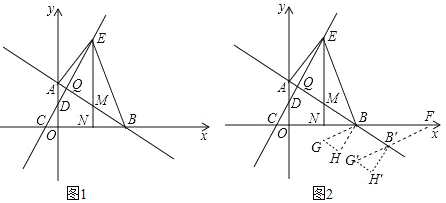
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】甲、乙兩人兩次同時在一家糧店購買大米,兩次大米的價格分別為每千克a元和b元(a≠b).甲每次買100千克大米,乙每次買100元大米.
(1)用含a、b的代數(shù)式表示:甲兩次購買大米共需付款 元,乙兩次共購買 千克大米.若甲兩次購買大米的平均單價為每千克Q1元,乙兩次購買大米的平均單價為每千克Q2元.則:Q1= ;Q2= .
(2)若規(guī)定誰兩次購糧的平均價格低,誰購糧的方式就更合理,請你判斷比較甲、乙兩人的購糧方式,哪一個更合理,并說明你的理由.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】一次函數(shù)![]() 和
和![]() 的圖象如圖所示,且
的圖象如圖所示,且![]() ,
,![]() .
.
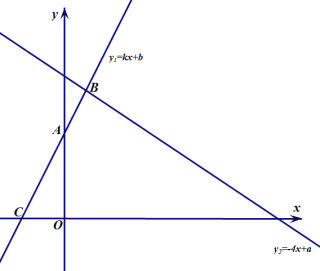
(1)由圖可知,不等式![]() 的解集是______;
的解集是______;
(2)若不等式![]() 的解集是
的解集是![]() .
.
①點![]() 的坐標為______.
的坐標為______.
②![]() 的值為_______.
的值為_______.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】某單位在疫情期間用 3000 元購進 A、B 兩種口罩1100 個,購買A種口罩與購買 B 種口罩的費用相同,且A種口罩的單價是 B 種口罩單價的 1.2 倍求 A,B 兩種口罩的單價各是多少元?
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com