已知x、y、z為實數,且x+y+z=5,xy+yz+zx=3,試求z的最大值與最小值.
【答案】
分析:由x+y+z=5得y=5-x-z代入,xy+yz+zx=3得x(5-x-z)+(5-x-z)z+zx=3整理得出關于x的一元二次方程x
2+(z-5)x+(z
2-5z+3)=0,利用關于x的一元二次方程的判別式得到關于z的不等式,解這個一元二次不等式可求得z的取值范圍.
解答:解:由x+y+z=5得y=5-x-z代入xy+yz+zx=3得
x(5-x-z)+(5-x-z)z+zx=3
5x-x
2-xz+5z-xz-z
2+zx-3=0,
整理得
x
2+(z-5)x+(z
2-5z+3)=0
因為x是實數,那么關于x的一元二次方程的判別式是(z-5)
2-4(z
2-5z+3)≥0
解這個一元二次不等式,
得-1≤z≤
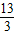
.
故z的最大值為
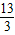
,最小值為-1.
點評:本題考查的是一元二次方程根與系數的關系,根據根的判別式以及不等式等知識點進行求解,考查學生的邏輯推理能力.

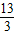 .
.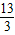 ,最小值為-1.
,最小值為-1.

 期末集結號系列答案
期末集結號系列答案