
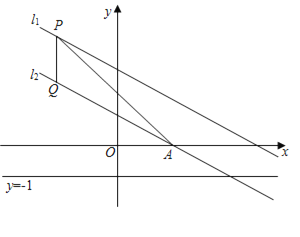
【題目】如圖,在平面直角坐標系中,直線l1:y=﹣![]() x+2向下平移1個單位后,得到直線l2,l2交x軸于點A,點P是直線l1上一動點,過點P作PQ∥y軸交l2于點Q
x+2向下平移1個單位后,得到直線l2,l2交x軸于點A,點P是直線l1上一動點,過點P作PQ∥y軸交l2于點Q
(1)求出點A的坐標;
(2)連接AP,當△APQ為以PQ為底邊的等腰三角形時,求點P和點Q的坐標;
(3)點B為OA的中點,連接OQ、BQ,若點P在y軸的左側,M為直線y=﹣1上一動點,當△PQM與△BOQ全等時,求點M的坐標.
【答案】(1)A(2,0);(2)P(3,![]() ),Q(3,﹣
),Q(3,﹣![]() );(3)M(﹣1,﹣1)或(﹣1,8)
);(3)M(﹣1,﹣1)或(﹣1,8)
【解析】
(1)求出直線l2的解析式為y=﹣![]() x+1,即可求A的坐標;
x+1,即可求A的坐標;
(2)設點P(x,﹣![]() x+2),Q(x,﹣
x+2),Q(x,﹣![]() x+1),由AQ=AP,即可求P點坐標;
x+1),由AQ=AP,即可求P點坐標;
(3)設P(n,﹣![]() n+2),M(m,﹣1),則Q(n,﹣
n+2),M(m,﹣1),則Q(n,﹣![]() n+1),可求出BQ=
n+1),可求出BQ=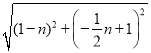 ,OQ=
,OQ=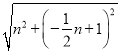 ,PM=
,PM=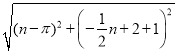 ,QM=
,QM=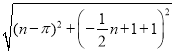 ,①當△PQM≌△BOQ時,PM=BQ,QM=OQ,結合勾股定理,求出m;②當△QPM≌△BOQ時,有PM=OQ,QM=BQ,結合勾股定理,求出m即可.
,①當△PQM≌△BOQ時,PM=BQ,QM=OQ,結合勾股定理,求出m;②當△QPM≌△BOQ時,有PM=OQ,QM=BQ,結合勾股定理,求出m即可.
解:(1)∵直線l1:y=﹣![]() x+2向下平移1個單位后,得到直線l2,
x+2向下平移1個單位后,得到直線l2,
∴直線l2的解析式為y=﹣![]() x+1,
x+1,
∵l2交x軸于點A,
∴A(2,0);
(2)當△APQ為以PQ為底邊的等腰三角形時,
∴AQ=AP,
∵點P是直線l1上一動點,
設點P(x,﹣![]() x+2),
x+2),
∵過點P作PQ∥y軸交l2于點Q
∴Q(x,﹣![]() x+1),
x+1),
∴(﹣![]() x+2)2=(﹣
x+2)2=(﹣![]() x+1)2,
x+1)2,
∴x=3,
∴P(3,![]() ),Q(3,﹣
),Q(3,﹣![]() );
);
(3)∵點B為OA的中點,
∴B(1,0),
∴PQ=BO=1,
設P(n,﹣![]() n+2),M(m,﹣1),則Q(n,﹣
n+2),M(m,﹣1),則Q(n,﹣![]() n+1),
n+1),
∴BQ=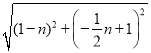 ,OQ=
,OQ=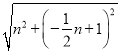 ,
,
PM=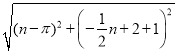 ,QM=
,QM=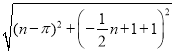 ,①
,①
∵△PQM與△BOQ全等,
①當△PQM≌△BOQ時,
有PM=BQ,QM=OQ,
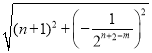 =
=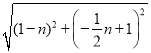 ,
,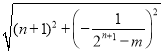 =
=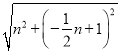 ,
,
∴n=2m﹣2,
∵點P在y軸的左側,
∴n<0,
∴m<1,
∴m=﹣1,
∴M(﹣1,﹣1);
②當△QPM≌△BOQ時,
有PM=OQ,QM=BQ,
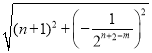 =
=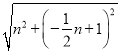 ,
,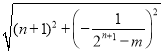 =
=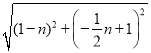 ,
,
∴n=![]() ﹣
﹣![]() m,
m,
∵點P在y軸的左側,
∴n<0,
∴m>2,
∴m=8,
∴M(﹣1,8);
綜上所述,M(﹣1,﹣1)或M(﹣1,8).1:y=﹣![]() x+2向下平移1個單位后,得到直線l2,
x+2向下平移1個單位后,得到直線l2,


科目:初中數學 來源: 題型:
【題目】如圖,已知△ABC,按以下步驟作圖:①分別以 B,C 為圓心,以大于![]() BC 的長為半徑作弧,兩弧相交于兩點 M,N;②作直線 MN 交 AB 于點 D,連接 CD.若 CD=AC,∠A=50°,則∠ACB 的度數為
BC 的長為半徑作弧,兩弧相交于兩點 M,N;②作直線 MN 交 AB 于點 D,連接 CD.若 CD=AC,∠A=50°,則∠ACB 的度數為
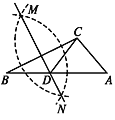
A.90°B.95°C.105°D.110°
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,將![]() ABCD的邊AB延長到點E,使BE=AB,連接DE,交邊BC于點F.
ABCD的邊AB延長到點E,使BE=AB,連接DE,交邊BC于點F.
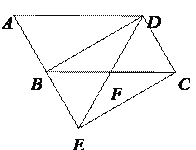
(1)求證:△BEF≌△CDF.
(2)連接BD,CE,若∠BFD=2∠A,求證四邊形BECD是矩形.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在一組數據![]() ,
,![]() ,
,![]() 中,各數據與它們的平均數
中,各數據與它們的平均數![]() 的差的絕對值的平均數,記作
的差的絕對值的平均數,記作![]() 叫做這組數據的“平均差”.一組數據的平均差越大,就說明這組數據的離散程度越大.則樣本:
叫做這組數據的“平均差”.一組數據的平均差越大,就說明這組數據的離散程度越大.則樣本:![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 的平均差是( )
的平均差是( )
A. ![]() B. 3 C. 6 D.
B. 3 C. 6 D. ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點P、Q分別是邊長為4cm的等邊△ABC邊AB、BC上的動點(端點除外),點P從頂點A,點Q從頂點B同時出發,且它們的速度都為1cm/s,連接AQ、CP交于點M,則在P、Q運動的過程中,
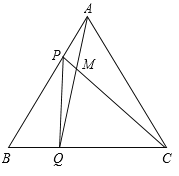
(1)求證:△ABQ ≌ △CAP;
(2)∠CMQ的大小變化嗎?若變化,則說明理由,若不變,則求出它的度數;
(3)連接PQ,當點P、Q運動多少秒時,△APQ是等腰三角形?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某初中學校欲向高一級學校推薦一名學生,根據規定的推薦程序:首先由本年級200名學生民主投票,每人只能推薦一人(不設棄權票),選出了票數最多的甲、乙、丙三人.投票結果統計如圖一:

其次,對三名候選人進行了筆試和面試兩項測試.各項成績如右表所示:圖二是某同學根據上表繪制的一個不完整的條形圖.請你根據以上信息解答下列問題:
(1)補全圖一和圖二.
(2)請計算每名候選人的得票數.
(3)若每名候選人得一票記1分,投票、筆試、面試三項得分按照2:5:3的比確定,計算三名候選人的平均成績,成績高的將被錄取,應該錄取誰?
測試項目 | 測試成績/分 | ||
甲 | 乙 | 丙 | |
筆試 | 92 | 90 | 95 |
面試 | 85 | 95 | 80 |
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知![]() 在平面直角坐標系中的位置如圖所示,將
在平面直角坐標系中的位置如圖所示,將![]() 向右平移5個單位長度,再向下平移3個單位長度得到
向右平移5個單位長度,再向下平移3個單位長度得到![]() .(圖中每個小方格邊長均為1個單位長度)
.(圖中每個小方格邊長均為1個單位長度)
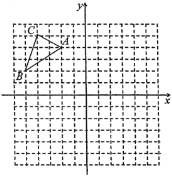
(1)在圖中畫出平移后的![]() ;
;
(2)直接寫出![]() 各頂點的坐標
各頂點的坐標![]() ______,
______,![]() ______,
______,![]() ______.
______.
(3)在![]() 軸上找到一點
軸上找到一點![]() ,當
,當![]() 取最小值時,
取最小值時,![]() 點的坐標是______.
點的坐標是______.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com