如圖，AB是⊙O的直徑，點C在⊙O上，過點C作⊙O的切線CM．
（1）求證：∠ACM=∠ABC；
（2）延長BC到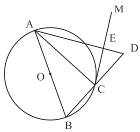
D，使BC = CD，連接AD與CM交于點E，若⊙O的半徑為3
，ED = 2, 
求∆ACE的外接圓的半徑．
證明：（1）連接OC
∵ AB為⊙O的直徑
∴ ∠ACB = 90°
∴ ∠ABC ＋∠BAC = 90°[來源:]
又∵ CM是⊙O的切線
∴ OC⊥CM
∴ ∠ACM ＋∠ACO = 90°
∵ CO = AO
∴ ∠BAC =∠ACO
∴ ∠ACM =∠ABC
（2）∵ BC = CD
∴ OC∥AD
又∵ OC⊥CE
∴ AD⊥CE
∴ ΔAEC是直角三角形
∴ ΔAEC的外接圓的直徑為AC
又∵ ∠ABC ＋∠BAC = 90°
∠ACM ＋∠ECD = 90°
而∠ABC =∠ACM
∴ ∠BAC =∠ECD
又∠CED =∠ACB = 90°
∴ ΔABC∽ΔCDE
∴ 
= 
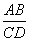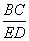
而⊙O的半徑為3
∴ AB = 6
∴ 
= 
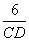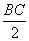
∴ BC2 = 12
∴ BC = 2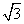
在RtΔABC中
∴ AC =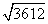 
= 2
∴ ΔAEC的外接圓的半徑為
輕松暑假總復習系列答案科目：初中數學 來源： 題型：
今年我市有4萬名學生參
加中考，為了了解這些考生的數學成績，從中抽取2000名考生的數學成績進行統計分析．在這個問題中，下列說法：
①這4萬名考生的數學中考成績的全體是總體；②每個考生是個體；③2000名考生是總體的一個樣本；④樣本容量是2000．
其中說法正確的有（ ）
A．4個 B． 3個 C． 2個 D． 1個
查看答案和解析>>
科目：初中數學 來源： 題型：
將兩個斜邊長相等的三角形紙片如圖①放置，其中∠ACB=∠CED=90°，∠A=45°，∠D=30°．把△DCE繞點C順時針旋轉15°得到△D1CE1，如圖②，連接D1B，則∠E1D1B的度數為（ ）
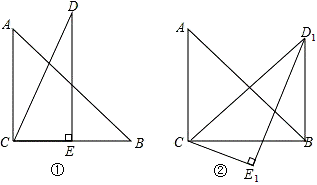
A．10° B． 20° C． 7.5° D． 15°
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
式的變形正確的是
B．
C．
D．
的圖像與反比例函數
的圖像交
于
兩點，點
的橫坐標為2．
的值和點
的象限，并說明理由．
，則該等腰三角形的底角的度數為___ __________．
，并依據a的取值情況寫出其解集．
> 
C、x+3>y+3 D、－3x>－3y
。