【題目】如圖，在平面直角坐標系中，一次函數
的圖象與反比例函數
的圖象交于C、D兩點， C點的坐標是（4，-1），D點的橫坐標為-2．
（1）求反比例函數與一次函數的關系式；
（2）根據圖象直接回答：當x為何值時，一次函數的值小于反比例函數的值？
活力試卷系列答案
課課優能力培優100分系列答案科目：初中數學 來源： 題型：
【題目】如圖，在ABCD中，∠BAD的角平分線交BC于點E，交DC的延長線于點F，連接DE．
（1）求證：DA＝DF；
（2）若∠ADE＝∠CDE＝30°，DE＝2
，求ABCD的面積．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】在一個不透明的盒子里，裝有三個分別標有數字1，2，4的小球，它們的形狀、大小、質地等完全相同，小明先從盒子里隨機取出一個小球，記下數字為x；放回盒子搖勻后，再由小華隨機取出一個小球，記下數字為y．
（1）寫出（x，y）的所有可能出現的結果；
（2）小明、小華各取一次，由取出小球所確定的數字作為點的坐標，這樣的點（x，y）中落在反比例函數y=
的圖象上的點的概率是多少？
查看答案和解析>>
科目：初中數學 來源： 題型：
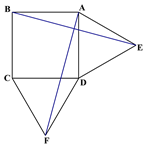
【題目】如圖1在正方形ABCD的外側作兩個等邊三角形ADE和DCF，連接AF，BE．
（圖1） （圖2） （備用圖）
（1）請判斷：AF與BE的數量關系是_____________，位置關系______________；
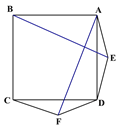
（2）如圖2，若將條件“兩個等邊三角形ADE和DCF”變為“兩個等腰三角形ADE和DCF，且EA=ED=FD=FC”，第（1）問中的結論是否仍然成立？請作出判斷并給予證明；
（3）若三角形ADE和DCF為一般三角形，且AE=DF，ED=FC，第（1）問中的結論都能成立嗎？請直接寫出你的判斷．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，一只甲蟲在5×5的方格（每小格邊長為1）上沿著網格線運動，它從A處出發去看望B、C、D處的其它甲蟲，規定：向上向右走為正，向下向左走為負．例如從A到B記為：A →B（+1，+3），從B到A記為：B→A（﹣1，-3），其中第一個數表示左右方向，第二個數表示上下方向．
（1）圖中A →C（______，______），B →C（______，______），C→_______（+1，﹣2）；
（2）若這只甲蟲的行走路線為A→B→C→D，請計算該甲蟲走過的路程；
（3）從A處去P處的行走路線依次為（+2，+2），（+2，﹣1），（﹣2，+3），（﹣1，﹣2），請在圖中標出P的位置；
（4）若圖中另有兩個格點M、N，且M→A（3-a，b-4），M→N（5-a，b-2），則N→A應記為什么？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】A、B兩地果園分別有橘子40噸和60噸，C、D兩地分別需要橘子30噸和70噸；已知從A、B到C、D的運價如表：
到C地 | 到D地 | |
A果園 | 每噸15元 | 每噸12元 |
B果園 | 每噸10元 | 每噸9元 |
（1）若從A果園運到C地的橘子為x噸，則從A果園運到D地的橘子為 噸，從A果園將橘子運往D地的運輸費用為 元.
（2）用含x的式子表示出總運輸費（要求：列式、化簡）
（3）若這批橘子在C地和D地進行再加工，經測算，全部橘子加工完畢后總成本為w元，且
.則當x= 時，w有最 值（填“大”或“小”），這個值是 .
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】我市某中學決定在學生中開展丟沙包、打籃球、跳大繩和踢毽球四種項目的活動，為了解學生對四種項目的喜歡情況，隨機調查了該校m名學生最喜歡的一種項目（每名學生必選且只能選擇四種活動項目的一種），并將調查結果繪制成如下的不完整的統計圖表：
學生最喜歡的活動項目的人數統計表
項目 | 學生數（名） | 百分比 |
丟沙包 | 20 | 10% |
打籃球 | 60 | p% |
跳大繩 | n | 40% |
踢毽球 | 40 | 20% |
根據圖表中提供的信息，解答下列問題：
（1）m= ，n= ，p= ；
（2）請根據以上信息直接補全條形統計圖；
（3）根據抽樣調查結果，請你估計該校2000名學生中有多少名學生最喜歡跳大繩．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】用火柴棒按下列方式搭建三角形：
（1）填表：
三角形個數 | 1 | 2 | 3 | 4 | … |
火柴棒根數 | … |
（2）當三角形的個數為
時，火柴棒的根數是多少？
（3）求當
時，有多少根火柴棒？
（4）當火柴棒的根數為2017時，三角形的個數是多少？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】閱讀下列材料：
解答“已知x﹣y=2，且x＞1，y＜0，試確定x+y的取值范圍”有如下解法
解：∵x﹣y=2，∴x=y+2 又∵x＞1∴y+2＞1∴y＞﹣1
又∵y＜0∴﹣1＜y＜0…①
同理可得1＜x＜2…②
由①+②得：﹣1+1＜x+y＜0+2∴x+y的取值范圍是0＜x+y＜2
按照上述方法，完成下列問題：
（1）已知x﹣y=3，且x＞2，y＜1，則x+y的取值范圍是
（2）已知關于x，y的方程組
的解都是正數
①求a的取值范圍；②若a﹣b=4，求a+b的取值范圍．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
