
【題目】小明有5張寫著不同的數字的卡片,請你按要求抽出卡片,完成下列各問題:
![]()
(1)從中取出2張卡片,使這2張卡片上數字乘積最大,最大值是 ;
(2)從中取出2張卡片,使這2張卡片上數字相除的商最小,最小值是 ;
(3)從中取出4張卡片,用學過的運算方法,使結果為24.寫出運算式子:
【答案】(1)15;(2)![]() ;(3)方法不唯一
;(3)方法不唯一
【解析】試題分析:(1)觀察這五個數,要找乘積最大的就要找符號相同且數值最大的數,所以選-3和-5;
(2)2張卡片上數字相除的商最小就要找符號不同,且分母越大越好,分子越小越好,所以就要選3和-5,且-5為分母;
(3)從中取出4張卡片,用學過的運算方法,使結果為24,這就不唯一,用加減乘除只要答數是24即可,比如-3、-5、0、3,四個數,{0-[(-3)+(-5)]}×3=24,再如:抽取-3、-5、3、4,則-[(-3)÷3+(-5)]×4=24.
試題解析:(1)(-3) ×(-5)=15;
(2)(5)÷(+3)= ![]() ;
;
(3)方法不唯一,如:抽取3、5、0、3,則{0[(3)+(5)]}×3=24;
如:抽取3、5、3、4,則[(3)÷3+(5)]×4=24.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
【題目】如圖,在矩形ABCD中,AB=8,BC=4,將矩形沿AC折疊,點D落在D′處,則重疊部分△AFC的面積是( ) 
A.8
B.10
C.20
D.32
查看答案和解析>>
科目:初中數學 來源: 題型:
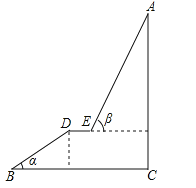
【題目】如圖,A為某旅游景區的最佳觀景點,游客可從B處乘坐纜車先到達小觀景平臺DE觀景,然后再由E處繼續乘坐纜車到達A處,返程時從A處乘坐升降電梯直接到達C處,已知:AC⊥BC于C,DE∥BC,BC=110米,DE=9米,BD=60米,α=32°,β=68°,求AC的高度.(參考數據:sin32°≈0.53;cos32°≈0.85;tan32°≈0.62;sin68°≈0.93;cos68°≈0.37;tan68°≈2.48)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】點A、B在數軸上分別表示有理數a、b,點A與原點O兩點之間的 距離表示為AO,則AO=|a-0|=|a|,類似地,點B與原點O兩點之間的距離表示 為BO,則BO=|b|,點A與點B兩點之間的距離表示為AB=|a-b|.請結合數軸,思考并回答以下問題:
(1)①數軸上表示1和-3的兩點之間的距離是__________;
②數軸上表示m和-1的兩點之間的距離是__________;
③數軸上表示m和-1的兩點之間的距離是3,則有理數m是___________;
(2)若x表示一個有理數,并且x比-3大,x比1小,則|x-1|+|x+3|=______;
(3)求滿足|x-2|+|x+4|=6的所有整數x的和.
![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(1)引入:
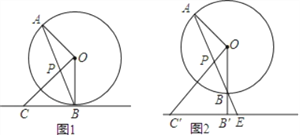
如圖1,直線AB為⊙O的弦,OC⊥OA,交AB于點P,且PC=BC,直線BC是否與⊙O相切,為什么?
(2)引申:
如圖2,記(1)中⊙O的切線為直線l,在(1)的條件下,將切線l向下平移,設平移后的直線l與OB的延長線相交于點B′,與AB的延長線相交于點E,與OP的延長線相交于點C′,找出圖2中與C′P相等的線段,并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知一元二次方程x2+ax+a-2=0.
(1)求證:不論a為何實數,此方程總有兩個不相等的實數根;
(2)設a<0,當二次函數y=x2+ax+a-2的圖象與x軸的兩個交點的距離為![]() 時,求出此二次函數的解析式;
時,求出此二次函數的解析式;
(3)在(2)的條件下,若此二次函數圖象與x軸交于A、B兩點,在函數圖象上是否存在點P,使得△PAB的面積為![]() ,若存在求出P點坐標,若不存在請說明理由.
,若存在求出P點坐標,若不存在請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com