Question

如圖，正方形ABCD中，有一直徑為BC的半圓，BC＝2cm，現有兩點E、F，分別從點B、點A同時出發，點E沿線段BA以1cm/s的速度向點A運動，點F沿折線A－D－C以2cm/s的速度向點C運動，設行進過程中點E離開點B的時間為t(秒)．

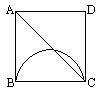
(1)當t為何值時，線段EF與BC平行？

(2)設1＜t＜2，當t為何值時，EF與半圓相切？

(3)當1≤t＜2時，設EF與AC相交于點P，問E、F運動時，點P的位置是否發生變化？若發生變化，說明理由，若不發生變化，請予以證明，并求AP∶PC的值．

Answer 1

答案：
解析：

(1)設E、F出發后，運動了t秒時，有EF∥BC，則BE＝t，CF＝4－2t，即有t＝4－2t，t＝，所以當t為秒時，線段EF與BC平行． 　　(2)設E、F出發后運動了t秒時，EF與半圓相切，過點F作KF∥BC交AB于K，則BE＝t，CF＝4－2t，EK＝t－(4－2t)＝3t－4，EF＝FB＋FC＝t＋(4－2t)＝4－t．又因為EF2＝EK2＋FK2，所以(4－t)2＝(3t－4)2＋22，2t2－4t＋1＝0，解得t＝．又1＜t＜2，所以t＝．所以，當t為秒時，EF與半圓相切． 　　(3)當1≤t＜2時，點P的位置不會發生變化．證明：設1≤t＜2時，E、F出發后運動了t秒鐘時，EF的位置如圖所示，則有BE＝t，AE＝2－t，CF＝4－2t，所以．又因為AB∥DC，所以△AEP∽△CFP． 　　所以，即點P的位置與t的取值無關，所以當1≤t＜2時，點P的位置不會發生變化，且AP∶PC的值為．