【答案】
分析:本題考查了一元二次方程的解法,解一元二次方程常用的方法有直接開平方法,配方法,公式法,因式分解法,要根據方程的特點靈活選用合適的方法.
(1)因方程移項可利用平方差公式分解,故用因式分解法;
(2)因方程系數特殊,可以用公式法求解;
(3)首先移項把常數項移到等號右邊,方程兩邊同時加上一次項系數一半的平方,則左邊是完全平方式,右邊是常數,即可求解;
(4)因方程有相同的部分可以用換元法代換,故用換元法求解.
解答:解:(1)將方程(3x-1)
2=(x+1)
2移項得,
(3x-1)
2-(x+1)
2=0,
∴(3x-1+x+1)(3x-1-x-1)=0,
∴4x(2x-2)=0,
∴x(x-1)=0,
解得x
1=0,x
2=1.
(2)∵2x
2+x-

=0,
可得,a=2,b=1,c=

,
∴x=-

±
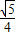
.
(3)∵x
2-4x+1=0,
∴(x-2)
2=3,
解得x
1=2+
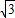
,x
2=2-
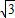
.
(4)設x
2+x=y,則y
2+y=6,y
1=-3,y
2=2,
則x
2+x=-3無解,
∴x
2+x=2,
解得x
1=-2,x
2=1.
點評:本題考查了解一元二次方程的方法,因式分解法是解一元二次方程的一種簡便方法,要會靈活運用,當化簡后不能用分解因式的方法即可考慮求根公式法,此法適用于任何一元二次方程.

 =0;
=0; =0,
=0, ,
, ±
±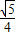 .
.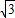 ,x2=2-
,x2=2-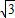 .
.
