
【題目】如圖是規格為![]() 的正方形網格,請在所給網格中按下列要求操作:
的正方形網格,請在所給網格中按下列要求操作:
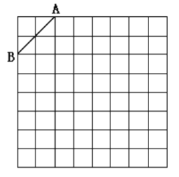
(1)請在網格中建立平面直角坐標系,使點![]() 坐標為
坐標為![]() ,
,![]() 點坐標為
點坐標為![]() ;
;
(2)在第二象限內的格點上畫一點![]() ,使點
,使點![]() 與線段
與線段![]() 組成一個以
組成一個以![]() 為底的等腰三角形,且腰長是無理數, 則
為底的等腰三角形,且腰長是無理數, 則![]() 點坐標是________,
點坐標是________,![]() 的周長是_________(結果保留根號);
的周長是_________(結果保留根號);
(3)畫出![]() 以點
以點![]() 為旋轉中心、旋轉
為旋轉中心、旋轉![]() 后的
后的![]() ,連結
,連結![]() 和
和![]() ,試說出四邊形
,試說出四邊形![]() 是何特殊四邊形, 并說明理由.
是何特殊四邊形, 并說明理由.
 陽光課堂課時優化作業系列答案
陽光課堂課時優化作業系列答案科目:初中數學 來源: 題型:
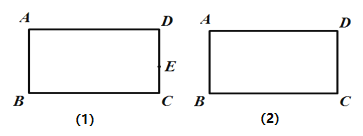
【題目】如圖,四邊形 ABCD 為矩形.
(1)如圖1,E為CD上一定點,在AD上找一點F,使得矩形沿著EF折疊后,點D落在 BC邊上(尺規作圖,保留作圖痕跡);
(2)如圖2,在AD和CD邊上分別找點M,N,使得矩形沿著MN折疊后BC的對應邊B' C'恰好經過點D,且滿足B' C' ⊥BD(尺規作圖,保留作圖痕跡);
(3)在(2)的條件下,若AB=2,BC=4,則CN= .
查看答案和解析>>
科目:初中數學 來源: 題型:
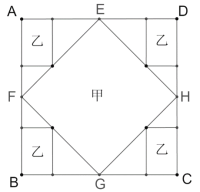
【題目】為了增加學校綠化,學校計劃建造一塊長為![]() 的正方形花壇
的正方形花壇![]() ,分別取四邊中點
,分別取四邊中點![]() ,構成四邊形
,構成四邊形![]() ,并計劃用“兩花一草”來裝飾,四邊形
,并計劃用“兩花一草”來裝飾,四邊形![]() 部分使用甲種花,在正方形
部分使用甲種花,在正方形![]() 四個角落構造4個全等的矩形區域種植乙種花,剩余部分種草坪,圖紙設計如下.
四個角落構造4個全等的矩形區域種植乙種花,剩余部分種草坪,圖紙設計如下.
(1)經了解,種植甲種花50元/![]() ,乙種花80元/
,乙種花80元/![]() ,草坪10元/
,草坪10元/![]() ,設一個矩形的面積為
,設一個矩形的面積為![]() ,裝飾總費用為
,裝飾總費用為![]() 元,求
元,求![]() 關于
關于![]() 的函數關系式.
的函數關系式.
(2)當裝飾費用為74880元時,則一個矩形區域的長和寬分別為多少?
(3)為了縮減開支,甲區域用單價為40元/![]() 的花,乙區域用單價為
的花,乙區域用單價為![]() 元/
元/![]() (
(![]() ,且
,且![]() 為10的倍數)的花,草坪單價不變,最后裝飾費只用了55000元,求
為10的倍數)的花,草坪單價不變,最后裝飾費只用了55000元,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中數學 來源: 題型:
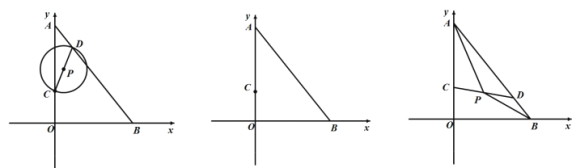
【題目】如圖,在平面直角坐標系![]() 中
中![]() ,點
,點![]() 從點
從點![]() 運動到點
運動到點![]() 停止,連接
停止,連接![]() ,以
,以![]() 長為直徑作
長為直徑作![]() .
.
(1)若![]() ,求
,求![]() 的半徑;
的半徑;
(2)當![]() 與
與![]() 相切時,求
相切時,求![]() 的面積;
的面積;
(3)連接![]() ,在整個運動過程中,
,在整個運動過程中,![]() 的面積是否為定值,如果是,請直接寫出面積的定值,如果不是,請說明理由.
的面積是否為定值,如果是,請直接寫出面積的定值,如果不是,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(1)閱讀理解
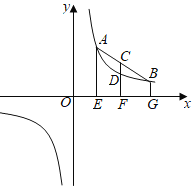
如圖,點![]() ,
,![]() 在反比例函數
在反比例函數![]() 的圖象上,連接
的圖象上,連接![]() ,取線段
,取線段![]() 的中點
的中點![]() .分別過點
.分別過點![]() ,
,![]() ,
,![]() 作
作![]() 軸的垂線,垂足為
軸的垂線,垂足為![]() ,
,![]() ,
,![]() ,
,![]() 交反比例函數
交反比例函數![]() 的圖象于點
的圖象于點![]() .點
.點![]() ,
,![]() ,
,![]() 的橫坐標分別為
的橫坐標分別為![]() ,
,![]() ,
,![]() .小紅通過觀察反比例函數
.小紅通過觀察反比例函數![]() 的圖象,并運用幾何知識得出結論:AE+BG=2CF,CF>DF,由此得出一個關于
的圖象,并運用幾何知識得出結論:AE+BG=2CF,CF>DF,由此得出一個關于![]() ,
,![]() ,
,![]() 之間數量關系的命題:若
之間數量關系的命題:若![]() ,則______.
,則______.
(2)證明命題
小東認為:可以通過“若![]() ,則
,則![]() ”的思路證明上述命題.
”的思路證明上述命題.
小晴認為:可以通過“若![]() ,
,![]() ,且
,且![]() ,則
,則![]() ”的思路證明上述命題.
”的思路證明上述命題.
請你選擇一種方法證明(1)中的命題.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,四邊形![]() 中,
中, ![]() ,過點
,過點![]() 作
作![]() 的平行線,交
的平行線,交![]() 于點
于點![]() ,交
,交![]() 于點
于點![]() .
.
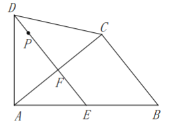
(1)求證:![]() 是
是![]() 的中點.
的中點.
(2)已知![]() ,
,![]() 是射線
是射線![]() 上的動點.設
上的動點.設![]() ,
,
①若四邊形![]() 的面積為
的面積為![]() ,求
,求![]() 關
關![]() 于的函數關系式;
于的函數關系式;
②在①中,當![]() 為何值時,
為何值時,![]() 的周長最小,并求出此時
的周長最小,并求出此時![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
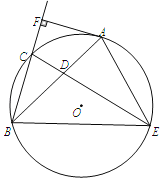
【題目】如圖,已知AB是⊙O的弦,點C是弧AB的中點,D是弦AB上一動點,且不與A、B重合,CD的延長線交于⊙O點E,連接AE、BE,過點A作AF⊥BC,垂足為F,∠ABC=30°.
(1)求證:AF是⊙O的切線;
(2)若BC=6,CD=3,則DE的長為 ;
(3)當點D在弦AB上運動時,![]() 的值是否發生變化?如果變化,請寫出其變化范圍;如果不變,請求出其值.
的值是否發生變化?如果變化,請寫出其變化范圍;如果不變,請求出其值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知矩形![]() 在
在![]() 上取兩點
上取兩點![]() (
(![]() 在
在![]() 左邊),以
左邊),以![]() 為邊作等邊三角形
為邊作等邊三角形![]() ,使頂點
,使頂點![]() 在
在![]() 上,
上,![]() 分別交
分別交![]() 于點
于點![]() .
.
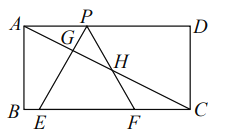
(1)求![]() 的邊長;
的邊長;
(2)在不添加輔助線的情況下,當![]() 與
與![]() 不重合時,從圖中找出一對相似三角形,并說明理由;
不重合時,從圖中找出一對相似三角形,并說明理由;
(3)若![]() 的邊
的邊![]() 在線段
在線段![]() 上移動.試猜想:
上移動.試猜想:![]() 與
與![]() 有何數量關系?并證明你猜想的結論.
有何數量關系?并證明你猜想的結論.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知二次函數![]() 的
的![]() 與
與![]() 的部分對應值如表:
的部分對應值如表:
|
|
|
|
|
|
|
|
|
|
|
|
下列結論:![]() 拋物線的開口向上;②拋物線的對稱軸為直線
拋物線的開口向上;②拋物線的對稱軸為直線![]() ;③當
;③當![]() 時,
時,![]() ;④拋物線與
;④拋物線與![]() 軸的兩個交點間的距離是
軸的兩個交點間的距離是![]() ;⑤若
;⑤若![]() 是拋物線上兩點,則
是拋物線上兩點,則![]() ,其中正確的個數是( )
,其中正確的個數是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com