
【題目】先閱讀下列材料,然后解答問題.
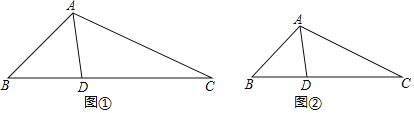
材料:從三角形(不是等腰三角形)一個頂點引出一條射線與對邊相交,頂點與交點之間的線段把這個三角形分割成兩個小三角形,如果分得的兩個小三角形中一個為等腰三角形,另一個與原三角形相似,我們把這條線段叫做這個三角形的完美分割線例如:如圖①,AD把△ABC分成△ABD與△ADC,若△ABD是等腰三角形,且△ADC∽△BAC,那么AD就是△ABC的完美分割線.
解答下列問題:
(1)如圖②,在△ABC中,∠B=40°,AD是△ABC的完美分割線,且△ABD是以AD為底邊的等腰三角形,則∠CAD= 度.
(2)在△ABC中,∠B=42°,AD是△ABC的完美分割線,且△ABD是等腰三角形,求∠BAC的度數.
【答案】(1)40;(2)∠BAC的度數為84°或111°
【解析】
(1)利用三角形的完美分割線定義可求解;
(2)分三種情況討論,由三角形的完美分割線定義和等腰三角形的性質可求解.
解:(1)∵AD是△ABC的完美分割線,
∴△DAC∽△ABC
∴∠CAD=∠B=40°
故答案為:40
(2)若BD=AD,
∵AD是△ABC的完美分割線,
∴△DAC∽△ABC
∴∠CAD=∠B=42°
∵AD=BD,
∴∠ABD=∠BAD=42°
∴∠BAC=∠BAD+∠CAD=84°
若AB=BD,
∴∠BAD=69°=∠BDA
∵∵AD是△ABC的完美分割線,
∴△DAC∽△ABC
∴∠CAD=∠B=42°
∴∠BAC=∠BAD+∠CAD=42°+69°=111°
若AB=AD,
∴∠B=∠ADB=42°
∵AD是△ABC的完美分割線,
∴△DAC∽△ABC
∴∠CAD=∠B=42°
∵∠ADB=∠DAC+∠C=42°+∠C≠42°
∴不存在AB=AD,
綜上所述:∠BAC的度數為84°或111°


科目:初中數學 來源: 題型:
【題目】如圖①,已知拋物線y=ax2﹣4amx+3am2(a、m為參數,且a>0,m>0)與x軸交于A、B兩點(A在B的左邊),與y軸交于點C.
(1)求點B的坐標(結果可以含參數m);
(2)連接CA、CB,若C(0,3m),求tan∠ACB的值;
(3)如圖②,在(2)的條件下,拋物線的對稱軸為直線l:x=2,點P是拋物線上的一個動點,F是拋物線的對稱軸l上的一點,在拋物線上是否存在點P,使△POF成為以點P為直角頂點的的等腰直角三角形.若存在,求出所有符合條件的點P的坐標,若不存在,請說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,拋物線y=ax2+bx+c(a≠0)的頂點和該拋物線與y軸的交點在一次函數y=kx+1(k≠0)的圖象上,它的對稱軸是x=1.有下列四個結論,①. abc<0; ②. a<-![]() ;③. a=-k;④. 當0<x<1時,ax+b>k,其中正確結論的個數是( )
;③. a=-k;④. 當0<x<1時,ax+b>k,其中正確結論的個數是( )
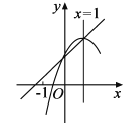
A.1;B.2C.3D.4
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖坐標系中,O(0,0),A(6,6![]() ),B(12,0),將△OAB沿直線CD折疊,使點A恰好落在線段OB上的點E處,若OE=
),B(12,0),將△OAB沿直線CD折疊,使點A恰好落在線段OB上的點E處,若OE=![]() ,則AC:AD的值是( )
,則AC:AD的值是( )
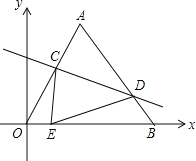
A.1:2B.2:3C.6:7D.7:8
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為宣傳“掃黑除惡”專項行動,社區準備制作一幅宣傳版面,噴繪時為了美觀,要在矩形圖案四周外圍增加一圈等寬的白邊,已知圖案的長為2米,寬為1米,圖案面積占整幅宣傳版面面積的90%,若設白邊的寬為x米,則根據題意可列出方程( )

A. 90%×(2+x)(1+x)=2×1 B. 90%×(2+2x)(1+2x)=2×1
C. 90%×(2﹣2x)(1﹣2x)=2×1 D. (2+2x)(1+2x)=2×1×90%
查看答案和解析>>
科目:初中數學 來源: 題型:
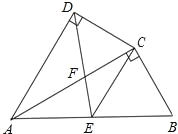
【題目】如圖,四邊形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E為AB的中點,
(1)求證:AC2=ABAD;
(2)求證:△AFD∽△CFE.
查看答案和解析>>
科目:初中數學 來源: 題型:
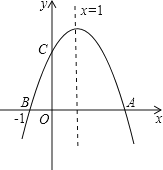
【題目】如圖,二次函數y=ax2+bx+c(a≠0)的圖象與x軸交于A,B兩點,與y軸交于C點,且對稱軸為x=1,點B坐標為(﹣1,0),則下面的四個結論,其中正確的個數為( )
①2a+b=0②4a﹣2b+c<0③ac>0④當y>0時,﹣1<x<4
A.1個B.2個C.3個D.4個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知拋物線![]() 與x軸交于點A、B(點A位于點B的左側),與y軸交于點C,CD∥x軸交拋物線于點D,M為拋物線的頂點.
與x軸交于點A、B(點A位于點B的左側),與y軸交于點C,CD∥x軸交拋物線于點D,M為拋物線的頂點.


(1)求點A、B、C的坐標;
(2)設動點N(-2,n),求使MN+BN的值最小時n的值;
(3)P是拋物線上一點,請你探究:是否存在點P,使以P、A、B為頂點的三角形與△ABD相似,(△PAB與△ABD不重合)?若存在,求出點P的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
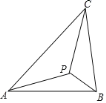
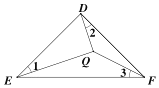
【題目】如圖所示,若△ABC內一點P滿足∠PAC=∠PBA=∠PCB,則點P為△ABC的布洛卡點,三角形的布洛卡點是法國數學家長數學教育家克洛爾于1816年首次發現,但他的發現并未被當時的人們所注意,1875年,布洛卡點被一個數學愛好者法國軍官布洛卡重新發現,并用他的名字命名.問題:已知在等腰直角三角形DEF中,∠EDF=90°,若點Q為△DEF的布洛卡點,DQ=1,則EQ+FQ=______________ .
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com