
【題目】已知拋物線![]() 與
與![]() 軸交于
軸交于![]() ,
,![]() 兩點,與
兩點,與![]() 軸交于點
軸交于點![]() .
.
(1)填空:![]() ,
,![]() .
.
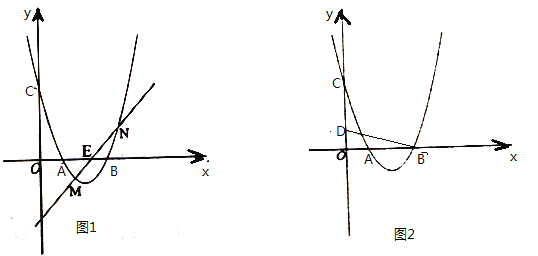
(2)如圖1,已知![]() ,過點
,過點![]() 的直線與拋物線交于點
的直線與拋物線交于點![]() 、
、![]() ,且點
,且點![]() 、
、![]() 關于點
關于點![]() 對稱,求直線
對稱,求直線![]() 的解析式.
的解析式.
(3)如圖2,已知![]() ,
,![]() 是第一象限內拋物線上一點,作
是第一象限內拋物線上一點,作![]() 軸于點
軸于點![]() ,若
,若![]() 與
與![]() 相似,請求出點
相似,請求出點![]() 的橫坐標.
的橫坐標.
【答案】(1)![]() ,
,![]() ;(2)直線
;(2)直線![]() ;(3)
;(3)![]() 點的橫坐標為
點的橫坐標為![]() 或
或![]()
【解析】
(1)把![]() ,
,![]() 代入解析式即可求出a,b的值;
代入解析式即可求出a,b的值;
(2)設直線MN為y=kx-![]() ,根據二次函數聯立得到一元二次方程,設交點
,根據二次函數聯立得到一元二次方程,設交點![]() 、
、![]() 的橫坐標為x1,x2,根據對稱性可得x1+x2=5,根據根與系數的關系求解k,即可求解.
的橫坐標為x1,x2,根據對稱性可得x1+x2=5,根據根與系數的關系求解k,即可求解.
(3)求出OD,OB,設P(x,![]() ),得到HP=x,DH=
),得到HP=x,DH=![]() -1=
-1=![]() ,根據
,根據![]() 與
與![]() 相似分兩種情況列出比例式即可求解.
相似分兩種情況列出比例式即可求解.
(1)把![]() ,
,![]() 代入
代入![]()
得![]() 解得
解得![]()
故答案為:-4;3;
(2)設直線MN為y=kx+b,把![]() 代入得b=-
代入得b=-![]()
∴直線MN為y=kx-![]() ,
,
聯立二次函數得kx-![]() =
=![]()
整理得x2-(k+4)x+![]() +3=0
+3=0
設交點![]() 、
、![]() 的橫坐標為x1,x2,
的橫坐標為x1,x2,
∵點![]() 、
、![]() 關于點
關于點![]() 對稱,
對稱,
∴x1+x2=5
故k+4=5
解得k=1
∴直線![]() ;
;
(3)∵D(0,1),B(3,0)
∴OD=1,OB=3,
設P(x,![]() ),
),
則HP=x,DH=![]() -1=
-1=![]() ,
,
當![]() ∽
∽![]() 時,
時,![]() ,即
,即![]()
解得x=![]()
當![]() ∽
∽![]() 時,
時,![]() ,即
,即![]()
解得x=![]()
∴![]() 點的橫坐標為
點的橫坐標為![]() 或
或![]() .
.



 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
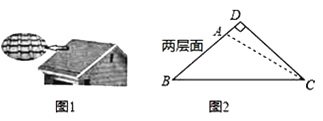
【題目】太陽能光伏建筑是現代綠色環保建筑之一,老張準備把自家屋頂改建成光伏瓦面,改建前屋頂截面△ABC如圖2所示,BC=10米,∠ABC=∠ACB=36°,改建后頂點D在BA的延長線上,且∠BDC=90°,求改建后南屋面邊沿增加部分AD的長.(結果精確到0.1米)
(參考數據:sin18°≈0.31,cos18°≈0.95.tan18°≈0.32,sin36°≈0.59.cos36°≈0.81,tan36°≈0.73)
查看答案和解析>>
科目:初中數學 來源: 題型:
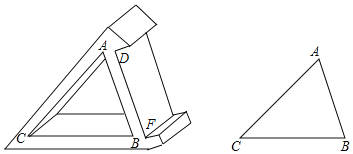
【題目】在全校的科技制作大賽中,王浩同學用木板制作了一個帶有卡槽的三角形手機架.如圖所示,卡槽的寬度DF與內三角形ABC的AB邊長相等.已知AC=20cm,BC=18cm,∠ACB=50°,一塊手機的最長邊為17cm,王浩同學能否將此手機立放入卡槽內?請說明你的理由(參考數據:sin50°≈0.8,cos50°≈0.6,tan50°≈1.2)
查看答案和解析>>
科目:初中數學 來源: 題型:
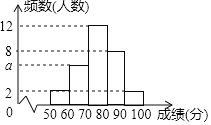
【題目】為了解某次“小學生書法比賽”的成績情況,隨機抽取了30名學生的成績進行統計,并將統計情況繪成如圖所示的頻數分布直方圖,己知成績x(單位:分)均滿足“50≤x<100”.根據圖中信息回答下列問題:
(1)圖中a的值為 ;
(2)若要繪制該樣本的扇形統計圖,則成績x在“70≤x<80”所對應扇形的圓心角度數為 度;
(3)此次比賽共有300名學生參加,若將“x≥80”的成績記為“優秀”,則獲得“優秀“的學生大約有 人:
(4)在這些抽查的樣本中,小明的成績為92分,若從成績在“50≤x<60”和“90≤x<100”的學生中任選2人,請用列表或畫樹狀圖的方法,求小明被選中的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1是小區常見的漫步機,從側面看如圖2,踏板靜止時,踏板連桿與立柱![]() 上的線段
上的線段![]() 重合,
重合,![]() 長為0.2米,當踏板連桿繞著點
長為0.2米,當踏板連桿繞著點![]() 旋轉到
旋轉到![]() 處時,測得
處時,測得![]() ,此時點
,此時點![]() 距離地面的高度
距離地面的高度![]() 為0.44米.求:
為0.44米.求:

(1)踏板連桿![]() 的長.
的長.
(2)此時點![]() 到立柱
到立柱![]() 的距離.(參考數據:
的距離.(參考數據:![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:初中數學 來源: 題型:
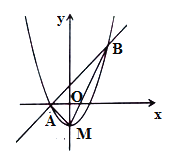
【題目】如圖,拋物線![]() 的頂點為
的頂點為![]() ,且拋物線與直線
,且拋物線與直線![]() 相交于
相交于![]() 兩點,且點
兩點,且點![]() 在
在![]() 軸上,點
軸上,點![]() 的坐標為
的坐標為![]() ,連接
,連接![]() .
.
(1)![]() ,
,![]() ,
,![]() (直接寫出結果);
(直接寫出結果);
(2)當![]() 時,則
時,則![]() 的取值范圍為 (直接寫出結果);
的取值范圍為 (直接寫出結果);
(3)在直線![]() 下方的拋物線上是否存在一點
下方的拋物線上是否存在一點![]() ,使得
,使得![]() 的面積最大?若存在,求出
的面積最大?若存在,求出![]() 的最大面積及點
的最大面積及點![]() 坐標.
坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
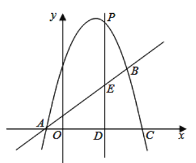
【題目】如圖,拋物線![]() 與直線
與直線![]() 相交于
相交于![]() ,
,![]() 兩點,且拋物線經過點
兩點,且拋物線經過點![]()
(1)求拋物線的解析式.
(2)點![]() 是拋物線上的一個動點(不與點
是拋物線上的一個動點(不與點![]() 點
點![]() 重合),過點
重合),過點![]() 作直線
作直線![]() 軸于點
軸于點![]() ,交直線
,交直線![]() 于點
于點![]() .當
.當![]() 時,求
時,求![]() 點坐標;
點坐標;
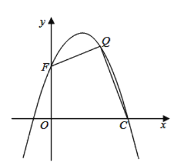
(3)如圖所示,設拋物線與![]() 軸交于點
軸交于點![]() ,在拋物線的第一象限內,是否存在一點
,在拋物線的第一象限內,是否存在一點![]() ,使得四邊形
,使得四邊形![]() 的面積最大?若存在,請求出點
的面積最大?若存在,請求出點![]() 的坐標;若不存在,說明理由.
的坐標;若不存在,說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】△ABC在平面直角坐標系中如圖:
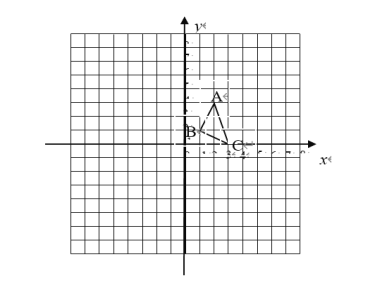
(1)畫出將△ABC繞點O逆時針旋轉90°所得到的![]() ,并寫出
,并寫出![]() 點的坐標.
點的坐標.
(2)畫出將△ABC關于x軸對稱的![]() ,并寫出
,并寫出![]() 點的坐標.
點的坐標.
(3)求在旋轉過程中線段OA掃過的圖形的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】“垃圾分類”越來越受到人們的關注,我市某中學對部分學生就“垃圾分類”知識的了解程度,采用隨機抽樣調查的方式,并根據收集到的信息進行統計,繪制了下面兩幅尚不完整的統計圖.根據圖中信息回答下列問題:
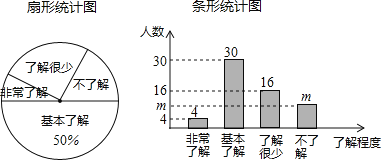
(1)接受問卷調查的學生共有 人,條形統計圖中![]() 的值為 ;
的值為 ;
(2)扇形統計圖中“了解很少”部分所對應扇形的圓心角的度數為 ;
(3)若從對垃圾分類知識達到“非常了解”程度的2名男生和2名女生中隨機抽取2人參加垃圾分類知識競賽,請用列表或畫樹狀圖的方法,求恰好抽到1名男生和1名女生的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com