
【題目】明明利用自制“四旋翼”無人機進行數學研究活動,無人機傳遞數據顯示,無人機A與地面CD的距離為420米,從無人機底部A處看“河南大玉米”(鄭州會展中心千禧大夏)頂部B的俯角為30°,看這棟大樓底部C的俯角為60°,求“河南大玉米”的高度.(![]() ,
,![]() ,
,![]() ≈2.236,結果精確到1m.)
≈2.236,結果精確到1m.)

 七星圖書口算速算天天練系列答案
七星圖書口算速算天天練系列答案科目:初中數學 來源: 題型:
【題目】已知二次函數![]() ,完成下列各題:
,完成下列各題:

![]() 將函數關系式用配方法化為
將函數關系式用配方法化為![]() 的形式,并寫出它的頂點坐標、對稱軸.
的形式,并寫出它的頂點坐標、對稱軸.
![]() 求出它的圖象與坐標軸的交點坐標.
求出它的圖象與坐標軸的交點坐標.
![]() 在直角坐標系中,畫出它的圖象.
在直角坐標系中,畫出它的圖象.
![]() 根據圖象說明:當
根據圖象說明:當![]() 為何值時,
為何值時,![]() ;當
;當![]() 為何值時,
為何值時,![]() .
.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】有一張等腰三角形紙片,AB=AC=5,BC=3,小明將它沿虛線PQ剪開,得到△AQP和四邊形BCPQ兩張紙片(如圖所示),且滿足∠BQP=∠B,則下列五個數據![]() ,3,
,3,![]() ,2,
,2,![]() 中可以作為線段AQ長的有_____個.
中可以作為線段AQ長的有_____個.
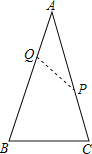
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知二次函數y=x2+bx+c的圖象經過點(4,3),(3,0).
(1)求b、c的值;
(2)求出該二次函數圖象的頂點坐標和對稱軸,并在所給坐標系中畫出該函數的圖象;
(3)該函數的圖象經過怎樣的平移得到y=x2的圖象?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖AB是⊙O的切線,切點為B,AO交⊙O于點C,過點C作DC⊥OA,交AB于點D.
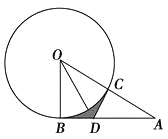
(1)求證:∠CDO=∠BDO;
(2)若∠A=30°,⊙O的半徑為4,求陰影部分的面積(結果保留π).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,Rt△ABC中,∠C=90°,BC=8cm,AC=6cm.點P從B出發沿BA向A運動,速度為每秒1cm,點E是點B以P為對稱中心的對稱點,點P運動的同時,點Q從A出發沿AC向C運動,速度為每秒2cm,當點Q到達頂點C時,P,Q同時停止運動,設P,Q兩點運動時間為t秒.
(1)當t為何值時,PQ∥BC?
(2)設四邊形PQCB的面積為y,求y關于t的函數關系式;
(3)四邊形PQCB面積能否是△ABC面積的![]() ?若能,求出此時t的值;若不能,請說明理由;
?若能,求出此時t的值;若不能,請說明理由;
(4)當t為何值時,△AEQ為等腰三角形?(直接寫出結果)
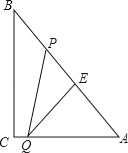
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了“創建文明城市,建設美麗家園”,我市某社區將轄區內的一塊面積為1000m2的空地進行綠化,一部分種草,剩余部分栽花,設種草部分的面積為![]() (m2),種草所需費用
(m2),種草所需費用![]() 1(元)與
1(元)與![]() (m2)的函數關系式為
(m2)的函數關系式為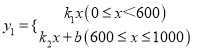 ,其圖象如圖所示:栽花所需費用
,其圖象如圖所示:栽花所需費用![]() 2(元)與x(m2)的函數關系式為
2(元)與x(m2)的函數關系式為![]() 2=﹣0.01
2=﹣0.01![]() 2﹣20
2﹣20![]() +30000(0≤
+30000(0≤![]() ≤1000).
≤1000).
(1)請直接寫出k1、k2和b的值;
(2)設這塊1000m2空地的綠化總費用為W(元),請利用W與![]() 的函數關系式,求出綠化總費用W的最大值;
的函數關系式,求出綠化總費用W的最大值;
(3)若種草部分的面積不少于700m2,栽花部分的面積不少于100m2,請求出綠化總費用W的最小值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在ABCD中,以點4為圓心,AB長為半徑畫弧交AD于點F;再分別以點B、F為圓心,大于![]() BF的長為半徑畫弧,兩弧交于點P;連接AP并廷長交BC于點E,連接EF
BF的長為半徑畫弧,兩弧交于點P;連接AP并廷長交BC于點E,連接EF
(1)根據以上尺規作圖的過程,求證:四邊形ABEF是菱形;
(2)若AB=2,AE=2![]() ,求∠BAD的大小.
,求∠BAD的大小.
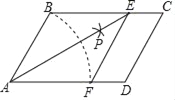
查看答案和解析>>
科目:初中數學 來源: 題型:
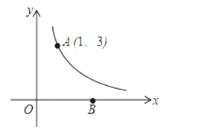
【題目】如圖,反比例函數y=![]() (k為常數,且k≠5)經過點A(1,3).
(k為常數,且k≠5)經過點A(1,3).
(1)求反比例函數的解析式;
(2)在x軸正半軸上有一點B,若△AOB的面積為6,求直線AB的解析式.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com