
【題目】如圖,在矩形ABCD中,AB=8cm,BC=6cm.動點P、Q分別從點A、C以2cm/s的速度同時出發.動點P沿AB向終點B運動,動點Q沿CD向終點D運動,連結PQ交對角線AC于點O.設點P的運動時間為t(s).

(1)求OC的長.
(2)當四邊形APQD是矩形時,直接寫出t的值.
(3)當四邊形APCQ是菱形時,求t的值.
(4)當△APO是等腰三角形時,直接寫出t的值.
【答案】(1)5;(2)t=2;(3)![]() ;(4)
;(4)![]() 或
或![]() 或
或![]()
【解析】
(1)根據矩形的性質以及勾股定理判定![]() ≌
≌![]() ,即可得解;
,即可得解;
(2)根據題意判定當四邊形APQD是矩形時,P、Q分別為AB、CD的中點,即可得解;
(3)根據菱形的性質以及勾股定理的運用,構建一元二次方程,即可得解;
(4)分情況:當AO=OP時,當AO=AP時,當AP=OP時,求解即可.
(1)∵四邊形ABCD是矩形,
∴![]() .
.
∴![]() ,
,![]() .
.
在Rt△ABC中,∠B=90°,
由勾股定理,得![]() .
.
∵![]() ,
,
∴![]() ≌
≌![]() .
.
∴![]() .
.
(2)當四邊形APQD是矩形時,P、Q分別為AB、CD的中點
即![]() =4
=4
t=2.
(3)如圖,當四邊形APCQ是菱形時,AP=CP=2t.

∴PB=8-2t.
在Rt△BCP中,∠B=90°,
由勾股定理,得![]() .
.
∴![]() .
.
解得![]() .
.
當![]() 時,四邊形APCQ是菱形.
時,四邊形APCQ是菱形.
(4)當AO=OP時,如圖所示:
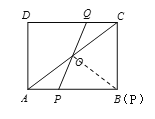
∵AO=5
∴P運動到點B
∴![]() ;
;
當AO=AP時,

∵AO=AP=5
∴![]() ;
;
當AP=OP時,
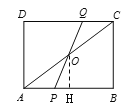
由(2),得OH=3,AH=4
∴PH=4-2t,OP=2t
∴![]() ,即
,即![]()
∴![]()
綜上所述,![]() 或
或![]() 或
或![]() .
.


科目:初中數學 來源: 題型:
【題目】已知,△ABC(如圖).
(1)利用尺規按下列要求作圖(保留作圖痕跡,不寫作法):
①作∠BAC的平分線AD,交BC于點D;
②作AB邊的垂直平分線EF,分別交AD,AB于點E,F.
(2)連接BE,若∠ABC=60°,∠C=40°,求∠AEB的度數.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在ABCD中,對角線AC、BD相交于O,EF過點O,且AF⊥BC.
(1)求證:△BFO≌△DEO;
(2)若EF平分∠AEC,試判斷四邊形AFCE的形狀,并證明.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀下面材料并解決問題
我們在分析解決某些數學問題時,經常要比較兩個數或代數式的大小而解決問題的策略般要進行一定的轉化,其中“求差法”就是常用的方法之一,所謂“求差法”:就是通過求差、變形,并利用差的符號來確定它們的大小,即要比較代數式![]() 的大小,只要求出它們的差
的大小,只要求出它們的差![]() ,若
,若![]() ,則
,則![]() ;若
;若![]() ,則
,則![]() .若
.若![]() ,則
,則![]() ,
,
請你用“求差法”解決以下問題
(1)若P=m2-2m-3,Q=m2-2m-1,比較![]() 的大小關系;
的大小關系;
(2)制作某產品有兩種用料方案方案一:用3塊![]() 型鋼板,用7塊
型鋼板,用7塊![]() 型鋼板;方案二:用2塊
型鋼板;方案二:用2塊![]() 型鋼板,用8塊
型鋼板,用8塊![]() 型鋼板;
型鋼板;![]() 型鋼板的面積比
型鋼板的面積比![]() 型鋼板的面積大,設每塊
型鋼板的面積大,設每塊![]() 型鋼板的面積為
型鋼板的面積為![]() ,每塊B型鋼板的面積為
,每塊B型鋼板的面積為![]() ,從省料角度考慮,應選哪種方案?
,從省料角度考慮,應選哪種方案?
(3)試比較圖1和圖2中兩個矩形周長![]() 、
、![]() 的大小.
的大小.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某中學計劃購買![]() 型和
型和![]() 型課桌凳共
型課桌凳共![]() 套,經招標,購買一套
套,經招標,購買一套![]() 型課桌凳比購買一套
型課桌凳比購買一套![]() 型課桌凳少用
型課桌凳少用![]() 元,且購買
元,且購買![]() 套
套![]() 型和
型和![]() 套
套![]() 型課桌凳共需
型課桌凳共需![]() 元.
元.
(1)求購買一套![]() 型課桌凳和一套
型課桌凳和一套![]() 型課桌凳各需多少元?
型課桌凳各需多少元?
(2)學校根據實際情況,要求購買這兩種課桌凳的總費用不能超過![]() 元,并且購買
元,并且購買![]() 型課桌凳的數量不能超過
型課桌凳的數量不能超過![]() 型課桌凳數量的
型課桌凳數量的![]() ,求該校本次購買
,求該校本次購買![]() 型和
型和![]() 型課桌凳共有幾種購買方案?怎樣的方案使總費用最低?并求出最低消費.
型課桌凳共有幾種購買方案?怎樣的方案使總費用最低?并求出最低消費.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,∠C=90°,AD是∠BAC的平分線,DE⊥AB于E,F在AC上,且BD=DF.
(1)求證:CF=EB;
(2)試判斷AB與AF,EB之間存在的數量關系,并說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某學校組織了“熱愛憲法,捍衛憲法”的知識競賽,賽后發現所有學生的成績(總分100分)均不低于50分,為了解本次競賽的成績分布情況,隨機抽取若干名學生的成績作為樣本進行整理,并繪制了不完整的統計圖表,請你根據統計圖表解答下列問題.
學校若干名學生成績分布統計表
分數段(成績為x分) | 頻數 | 頻率 |
50≤x<60 | 16 | 0.08 |
60≤x<70 | a | 0.31 |
70≤x<80 | 72 | 0.36 |
80≤x<90 | c | d |
90≤x≤100 | 12 | b |
(1)此次抽樣調查的樣本容量是 ;
(2)寫出表中的a= ,b= ,c= ;
(3)補全學生成績分布直方圖;
(4)比賽按照分數由高到低共設置一、二、三等獎,若有25%的參賽學生能獲得一等獎,則一等獎的分數線是多少?

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】海中有一個小島P,它的周圍18海里內有暗礁,漁船跟蹤魚群由西向東航行,在點A測得小島P在北偏東60°方向上,航行12海里到達B點,這時測得小島P在北偏東45°方向上.如果漁船不改變航線繼續向東航行,有沒有觸礁危險?請說明理由.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com