
| 3 |
| 3 |
| 3 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 22-12 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
| 3 |
| 42-22 |
| 3 |
| 3 |


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:
查看答案和解析>>
科目:初中數學 來源: 題型:
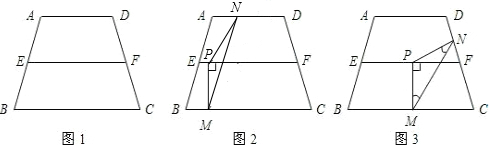
 條件時,其一定平分梯形的面積?(只要求說出條件,不需證明)
條件時,其一定平分梯形的面積?(只要求說出條件,不需證明)查看答案和解析>>
科目:初中數學 來源: 題型:
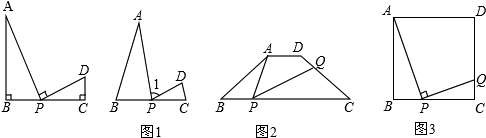
查看答案和解析>>
科目:初中數學 來源: 題型:
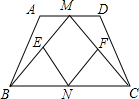 (2009•黔南州)楊老師在上四邊形時給學生出了這樣一個題.如圖,若在等腰梯形ABCD中,M、N分別是AD、BC的中點,E、F分別是BM、CM的中點時.提出以下問題:
(2009•黔南州)楊老師在上四邊形時給學生出了這樣一個題.如圖,若在等腰梯形ABCD中,M、N分別是AD、BC的中點,E、F分別是BM、CM的中點時.提出以下問題:查看答案和解析>>
科目:初中數學 來源: 題型:
| k | x |

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com