
【題目】(1)如圖①,AD是△ABC的中線.△ABD與△ACD的面積有怎樣的數量關系?為什么?
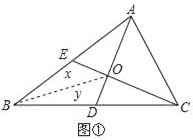
(2)若三角形的面積記為S,例如:△ABC的面積記為S△ABC.如圖②,已知S△ABC=1.△ABC的中線AD、CE相交于點O,求四邊形BDOE的面積.
小華利用(1)的結論,解決了上述問題,解法如下:
連接BO,設S△BEO=x,S△BDO=y,由(1)結論可得:S△BCE=S△BAD=![]() S△ABC=
S△ABC=![]() ,S△BCO=2S△BDO=2y,S△BAO=2S△BEO=2x.則有
,S△BCO=2S△BDO=2y,S△BAO=2S△BEO=2x.則有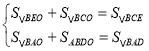 即
即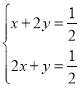 所以x+y=
所以x+y=![]() .即四邊形BDOE面積為
.即四邊形BDOE面積為![]() .
.
請仿照上面的方法,解決下列問題:
①如圖③,已知S△ABC=1.D、E是BC邊上的三等分點,F、G是AB邊上的三等分點,AD、CF交于點O,求四邊形BDOF的面積.
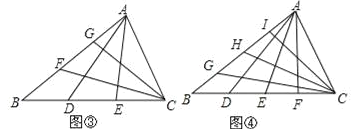
②如圖④,已知S△ABC=1.D、E、F是BC邊上的四等分點,G、H、I是AB邊上的四等分點,AD、CG交于點O,則四邊形BDOG的面積為 .
【答案】(1)S△ABD=S△ACD;(2)①![]() ,②
,②![]()
【解析】
(1)利用等底等高的三角形面積相等求解即可;
(2)①連接BO,設S△BDO=x,S△BGO=y,根據三角形間的面積關系列出方程組求解即可;
②連接BO,設S△BDO=x,S△BGO=y,根據三角形間的面積關系列出方程組求解即可.
解:(1)S△ABD=S△ACD.
∵AD是△ABC的中線,
∴BD=CD,
又∵△ABD與△ACD高相等,
∴S△ABD=S△ACD.
(2)①如圖3,連接BO,設S△BFO=x,S△BDO=y,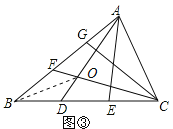
S△BCF=S△ABD=![]() S△ABC=
S△ABC=![]()
S△BCO=3S△BDO=3y,
S△BAO=3S△BFO=3x.
則有:![]() ,即
,即
所以x+y=![]() ,即四邊形BDOF的面積為
,即四邊形BDOF的面積為![]() ;
;
②如圖,連接BO,設S△BDO=x,S△BGO=y,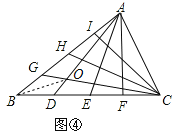
S△BCG=S△ABD=![]() S△ABC=
S△ABC=![]() ,
,
S△BCO=4S△BDO=4x,
S△BAO=4S△BGO=4y.
則有:![]() ,即
,即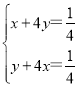
所以x+y=![]() ,即四邊形BDOG的面積為
,即四邊形BDOG的面積為![]() ,
,


 口算題卡加應用題集訓系列答案
口算題卡加應用題集訓系列答案科目:初中數學 來源: 題型:
【題目】已知正方形ABCD的邊長為6,E、F、P分別是AB、CD、AD上的點(均不與正方形頂點重合)且PE=PF,PE⊥PF.
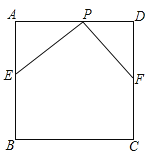
(1)求證:AE+DF=6
(2)設AE=![]() ,五邊形EBCFP的面積為
,五邊形EBCFP的面積為![]() ,求
,求![]() 與
與![]() 的函數關系式,并求出
的函數關系式,并求出![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】列代數式或方程解應用題:
![]() 已知小明的年齡是
已知小明的年齡是![]() 歲,小紅的年齡比小明的年齡的
歲,小紅的年齡比小明的年齡的![]() 倍小
倍小![]() 歲,小華的年齡比小紅的年齡大
歲,小華的年齡比小紅的年齡大![]() 歲,求這三名同學的年齡的和.
歲,求這三名同學的年齡的和.
![]() 小亮與小明從學校同時出發去看在首都體育館舉行的一場足球賽, 小亮每分鐘走
小亮與小明從學校同時出發去看在首都體育館舉行的一場足球賽, 小亮每分鐘走![]() ,他走到足球場等了
,他走到足球場等了![]() 分鐘比賽才開始:小明每分鐘走
分鐘比賽才開始:小明每分鐘走![]() ,他走到足球場,比賽已經開始了
,他走到足球場,比賽已經開始了![]() 分鐘.問學校與足球場之間的距離有多遠?
分鐘.問學校與足球場之間的距離有多遠?
![]() 請根據圖中提供的信息,回答下列問題:
請根據圖中提供的信息,回答下列問題:

①一個水瓶與一個水杯分別是多少元?
②甲、乙兩家商場都銷售該水瓶和水杯,為了迎接新年,兩家商場都在搞促銷活動,甲商場規定:這兩種商品都打八折;乙商場規定:買一個水瓶贈送兩個水杯,單獨購買的水杯仍按原價銷售.若某單位想在一家商場買![]() 個水瓶和
個水瓶和![]() 個水杯,請問選擇哪家商場更合算?請說明理由.
個水杯,請問選擇哪家商場更合算?請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
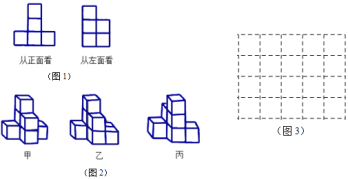
【題目】一個由若干小正方形堆成的幾何體,它從正面看和從左面看的圖形如圖1所示.
![]() 這個幾何體可以是圖2中甲,乙,丙中的______;
這個幾何體可以是圖2中甲,乙,丙中的______;
![]() 這個幾何體最多由______個小正方體堆成,最少由______個小正方體堆成;
這個幾何體最多由______個小正方體堆成,最少由______個小正方體堆成;
![]() 請在圖3中用陰影部分畫出符合最少情況時的一個從上面往下看得到的圖形.
請在圖3中用陰影部分畫出符合最少情況時的一個從上面往下看得到的圖形.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】請在下面括號里補充完整證明過程:
已知:如圖,△ABC中,∠ACB=90°,AF平分∠CAB,交CD于點E,交CB于點F,且∠CEF=∠CFE.求證:CD⊥AB.
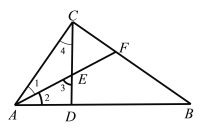
證明:∵AF平分∠CAB (已知)
∴ ∠1=∠2( )
∵∠CEF=∠CFE , 又∠3=∠CEF (對頂角相等)
∴∠CFE=∠3(等量代換)
∵在△ACF中,∠ACF=90°(已知)
∴( )+∠CFE=90°( )
∵∠1=∠2, ∠CFE=∠3(已證) ∴( )+( )=90°(等量代換)
在△AED中, ∠ADE=90°( 三角形內角和定理)
∴ CD⊥AB( ).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,四邊形ABCD中,∠BAD=100°,∠BCD=70°,點M,N分別在AB,BC上,將△BMN沿MN翻折,得△FMN,若MF∥AD,FN∥DC,求∠B的度數.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】探究:數軸上任意兩點之間的距離與這兩點對應的數的關系.
![]()
(1)如果點A表示數5,將點A先向左移動4個單位長度到達點B,那么點B表示的數是 ,A、B兩點間的距離是 .
如果點A表示數﹣2,將點A向右移動5個單位長度到達點B,那么點B表示的數是 ,A、B兩點間的距離是 .
(2)發現:在數軸上,如果點M對應的數是m,點N對應的數是n,那么點M與點N之間的距離可表示為 (用m、n表示,且m≥n).
(3)應用:利用你發現的結論解決下列問題:數軸上表示x和﹣2的兩點P與Q之間的距離是3,則x= .
查看答案和解析>>
科目:初中數學 來源: 題型:
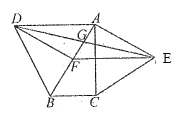
【題目】如圖,分別以![]() 的斜邊
的斜邊![]() ,直角邊
,直角邊![]() 為邊向外作等邊
為邊向外作等邊![]() 和
和![]() ,
,![]() 為
為![]() 的中點,
的中點,![]() ,
,![]() 相交于點
相交于點![]() .若∠BAC=30°,下列結論:①
.若∠BAC=30°,下列結論:①![]() ;②四邊形
;②四邊形![]() 為平行四邊形;③
為平行四邊形;③![]() ;④
;④![]() .其中正確結論的序號是______.
.其中正確結論的序號是______.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】隨著科技的進步和網絡資源的豐富,在線學習已成為更多人的自主學習選擇.某校計劃為學生提供以下四類在線學習方式:在線閱讀、在線聽課、在線答題和在線討論.為了解學生需求,該校隨機對本校部分學生進行了“你對哪類在線學習方式最感興趣”的調查,并根據調查結果繪制成如下兩幅不完整的統計圖.
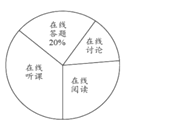
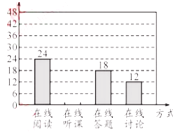
根據圖中信息,解答下列問題:
(1)求本次調查的學生總人數,并補全條形統計圖;
(2)求扇形統計圖中“在線討論”對應的扇形圓心角的度數;
(3)該校共有學生![]() 人,請你估計該校對在線閱讀最感興趣的學生人數.
人,請你估計該校對在線閱讀最感興趣的學生人數.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com