
【題目】如圖,⊙O為Rt△ABC的內切圓,⊙O的半徑r=1,∠B=30°,
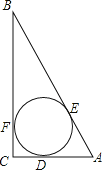
(1)劣弧DE的長.
(2)證明:AD=AE.
(3)求:劣弧DE、切線AD、AE所圍成的面積S.
【答案】(1)![]() (2)證明見解析(3)
(2)證明見解析(3)![]() ﹣
﹣![]()
【解析】
試題分析:(1)根據切線的性質得出OD⊥AC,OE⊥AB,根據四邊形內角和求得∠DOE=120°,代入公式求得即可;
(2)證得RT△AOD≌RT△AOE即可得到結論;
(3)根據S=S四邊形ADOE﹣S扇形ODE求得即可.
解:(1)連接OD、OE,則OD⊥A,COE⊥AB
∵∠B=30°∠C=90°
∴∠A=60°
∴∠DOE=120°
劣弧DE的長=![]() ;
;
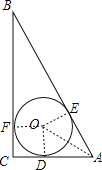
(2)連接OA,
在RT△AOD和RT△AOE中
![]()
∴RT△AOD≌RT△AOE(HL),
∴AD=AE
(3)∵RT△AOD≌RT△AOE,
∴∠OAB=∠OAC=![]() ∠BAC=30°,
∠BAC=30°,
∴AE=![]() OE=
OE=![]() ,
,
∴四邊形ADOE的面積=2×![]() AE
AE![]() OE=
OE=![]() ,
,
∵S扇形ODE=![]() =
=![]() π
π
∴S=S四邊形ADOE﹣S扇形ODE=![]() ﹣
﹣![]() .
.


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:
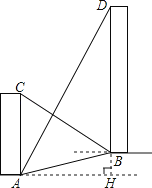
【題目】如圖,AC、BD是一斜坡AB上的兩幢樓房,斜坡AB的坡度是1:2![]() ,從點A測得樓BD頂部D處的仰角60°,從點B測得樓AC頂部C處的仰角30°,樓BD自身高度BD比樓AC高12米,求樓AC和樓BD之間的水平距離?(結果保留根號)
,從點A測得樓BD頂部D處的仰角60°,從點B測得樓AC頂部C處的仰角30°,樓BD自身高度BD比樓AC高12米,求樓AC和樓BD之間的水平距離?(結果保留根號)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某車間有26名工人,每人每天可以生產800個螺釘或1000個螺母,1個螺釘需要配2個螺母,為使每天生產的螺釘和螺母剛好配套.設安排x名工人生產螺釘,則下面所列方程正確的是( )
A.2×1000(26﹣x)=800x B.1000(13﹣x)=800x
C.1000(26﹣x)=2×800x D.1000(26﹣x)=800x
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,拋物線y=﹣x2+2x+3與x軸交于A,B,與y軸交于C,拋物線的頂點為D,直線l過C交x軸于E(4,0).
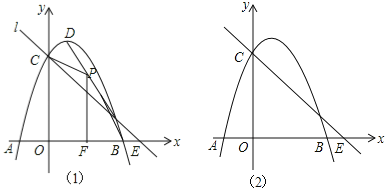
(1)寫出D的坐標和直線l的解析式;
(2)P(x,y)是線段BD上的動點(不與B,D重合),PF⊥x軸于F,設四邊形OFPC的面積為S,求S與x之間的函數關系式,并求S的最大值;
(3)點Q在x軸的正半軸上運動,過Q作y軸的平行線,交直線l于M,交拋物線于N,連接CN,將△CMN沿CN翻轉,M的對應點為M′.在圖2中探究:是否存在點Q,使得M′恰好落在y軸上?若存在,請求出Q的坐標;若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com