
 提分百分百檢測卷系列答案
提分百分百檢測卷系列答案 寶貝計劃期末沖刺奪100分系列答案
寶貝計劃期末沖刺奪100分系列答案 能考試全能100分系列答案
能考試全能100分系列答案科目:初中數學 來源: 題型:解答題

查看答案和解析>>
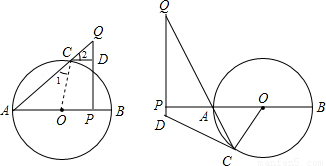
科目:初中數學 來源:第35章《圓(二)》中考題集(17):35.3 探索切線的性質(解析版) 題型:解答題
查看答案和解析>>
科目:初中數學 來源:第28章《圓》中考題集(50):28.2 與圓有關的位置關系(解析版) 題型:解答題

查看答案和解析>>
科目:初中數學 來源:第3章《直線與圓、圓與圓的位置關系》中考題集(16):3.1 直線與圓的位置關系(解析版) 題型:解答題

查看答案和解析>>
科目:初中數學 來源:第3章《圓》中考題集(44):3.5 直線和圓的位置關系(解析版) 題型:解答題

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com