
【題目】某市舉行知識大賽,A校、B校各派出5名選手組成代表隊參加決賽,兩校派出選手的決賽成績如圖所示.
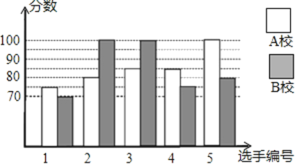
(1)根據圖示填寫下表:

(2)結合兩校成績的平均數和中位數,分析哪個學校的決賽成績較好;
(3)計算兩校決賽成績的方差,并判斷哪個學校代表隊選手成績較為穩定.
【答案】(1)見解析;(2)A校成績好些;(3)A校代表隊選手成績較為穩定.
【解析】
(1)根據平均數、眾數、中位數的概念以及求解方法分別進行計算補全統計表即可;
(2)根據平均數和中位數的統計意義分析得出即可;
(3)分別求出A校、B校的方差進而進行判斷即可.
(1)A校平均數為:![]() ×(75+80+85+85+100)=85,眾數85;
×(75+80+85+85+100)=85,眾數85;
B校成績按從小到大排序為:70、75、80、100、100,所以中位數為80,
填表如下:
平均數/分 | 中位數/分 | 眾數/分 | |
A校 | 85 | 85 | 85 |
B校 | 85 | 80 | 100 |
故答案為:85;85;80;
(2)A校成績好些.因為兩個隊的平均數都相同,A校的中位數高,
所以在平均數相同的情況下中位數高的A校成績好些;
(3)∵A校的方差
s12=![]() ×[(75﹣85)2+(80﹣85)2+(85﹣85)2+(85﹣85)2+(100﹣85)2]=70,
×[(75﹣85)2+(80﹣85)2+(85﹣85)2+(85﹣85)2+(100﹣85)2]=70,
B校的方差
s22=![]() ×[(70﹣85)2+(100﹣85)2+(100﹣85)2+(75﹣85)2+(80﹣85)2]=160,
×[(70﹣85)2+(100﹣85)2+(100﹣85)2+(75﹣85)2+(80﹣85)2]=160,
∴s12<s22,
因此,A校代表隊選手成績較為穩定.


科目:初中數學 來源: 題型:
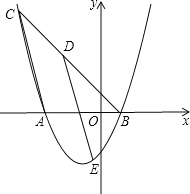
【題目】如圖,已知拋物線y=![]() x2+mx+n與x軸相交于點A、B兩點,過點B的直線y=x+b交拋物線于另一點C(-5,6),點D是線段BC上的一個動點(點D與點B、C不重合),作DE∥AC,交該拋物線于點E,
x2+mx+n與x軸相交于點A、B兩點,過點B的直線y=x+b交拋物線于另一點C(-5,6),點D是線段BC上的一個動點(點D與點B、C不重合),作DE∥AC,交該拋物線于點E,
(1)求m,n,b的值;
(2)求tan∠ACB;
(3)探究在點D運動過程中,是否存在∠DEA=45°,若存在,則求此時線段AE的長;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
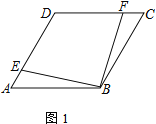
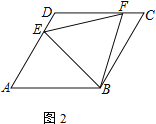
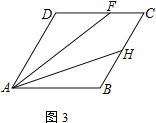
【題目】四邊形ABCD為菱形,點E在邊AD上,點F在邊CD上
(1) 若AE=CF,求證:EB=BF
(2) 若AD=4,DE=CF,且△EFB為等邊三角形,求四邊形DEBF的面積
(3) 若∠DAB=60°,點H在邊BC上,且BH=HC=2.若∠DFA=2∠HAB,直接寫出CF的長
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,半徑為1的圓O1與半徑為3的圓O2相內切,如果半徑為2的圓與圓O1和圓O2都相切,那么這樣的圓的個數是 ( )
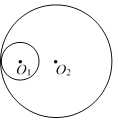
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,有一塊矩形紙片ABCD,AB=8,AD=6.將紙片折疊,使得AD邊落在AB邊上,折痕為AE,再將△AED沿DE向右翻折,AE與BC的交點為F,則CF的長為________

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(知識背景)在學習計算框圖時,可以用![]() 表示數據輸入、輸出框;
表示數據輸入、輸出框;![]() 用表示數據處理和運算框:用◇表示數據判斷框(根據條件決定執行兩條路徑中的某一條)
用表示數據處理和運算框:用◇表示數據判斷框(根據條件決定執行兩條路徑中的某一條)
(嘗試解決)
(1)①如圖1,當輸入數![]() 時,輸出數y=_________;
時,輸出數y=_________;
②如圖2,第一個“![]() ”內,應填_________;第二個“
”內,應填_________;第二個“![]() ”內,應填_________;
”內,應填_________;
(2)①如圖3,當輸入數![]() 時,輸出數
時,輸出數![]() =_________;
=_________;
②如圖4,當輸出的值![]() =26,則輸入的值
=26,則輸入的值![]() =_________;
=_________;
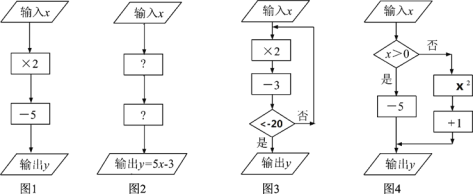
(實際應用)
(3)為鼓勵節約用水,決定對用水實行“階梯價”:當每月用水量不超過10噸時(含10噸),以3元/噸的價格收費;當每月用水量超過10噸時,超過部分以4元/噸的價格收費.請設計出一個“計算框圖”,使得輸入數為用水量![]() ,輸出數為水費
,輸出數為水費![]() .
.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,拋物線![]() 與x軸交于點A、B,與y軸交于點C,直線y=x+4經過點A、C,點P為拋物線上位于直線AC上方的一個動點.
與x軸交于點A、B,與y軸交于點C,直線y=x+4經過點A、C,點P為拋物線上位于直線AC上方的一個動點.
(1)求拋物線的表達式;
(2)如圖,當CP//AO時,求∠PAC的正切值;
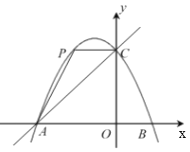
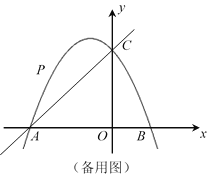
(3)當以AP、AO為鄰邊的平行四邊形第四個頂點恰好也在拋物線上時,求出此時點P的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校七年級共有800名學生,準備調查他們對“低碳”知識的了解程度.
(1)在確定調查方式時,團委設計了以下三種方案:
方案一:調查七年級部分女生;
方案二:調查七年級部分男生;
方案三:到七年級每個班去隨機調查一定數量的學生.
請問其中最具有代表性的一個方案是 ;
(2)團委采用了最具有代表性的調查方案,并用收集到的數據繪制出兩幅不完整的統計圖(如圖①、圖②所示),請你根據圖中信息,將兩個統計圖補充完整;

(3)在扇形統計圖中,“比較了解”所在扇形的圓心角的度數是 .
(4)請你估計該校七年級約有 名學生比較了解“低碳”知識.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在如圖所示的5×5的正方形網格中,每個小正方形的邊長均為1,按下列要求畫圖或填空;

(1)畫一條線段AB使它的另一端點B落在格點上(即小正方形的頂點),且AB=2![]() ;
;
(2)以(1)中的AB為邊畫一個等腰△ABC,使點C落在格點上,且另兩邊的長都是無理數;
(3)△ABC的周長為 ,面積為 .
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com