

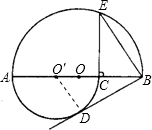
 ,
,
 k.
k.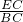 =
= ,
, ,
,

 靈星計算小達人系列答案
靈星計算小達人系列答案科目:初中數學 來源: 題型:
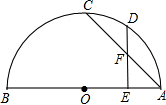 已知:如圖,AB為⊙O的直徑,C、D是半圓弧上的兩點,E是AB上除O外的一點,AC與DE相交于F.①
已知:如圖,AB為⊙O的直徑,C、D是半圓弧上的兩點,E是AB上除O外的一點,AC與DE相交于F.① |
| AD |
 |
| CD |
查看答案和解析>>
科目:初中數學 來源: 題型:
 =-
=-| 2 |
| 2 |
查看答案和解析>>
科目:初中數學 來源:2009-2010學年吉林省長春市外國語學校九年級(上)期中數學試卷(解析版) 題型:解答題
 ,②DE⊥AB,③AF=DF.
,②DE⊥AB,③AF=DF.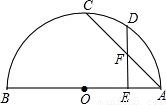
查看答案和解析>>
科目:初中數學 來源:2003年全國中考數學試題匯編《圓》(09)(解析版) 題型:解答題
 ,②DE⊥AB,③AF=DF.
,②DE⊥AB,③AF=DF.
查看答案和解析>>
科目:初中數學 來源:2003年四川省綿陽市中考數學試卷(解析版) 題型:解答題
 ,②DE⊥AB,③AF=DF.
,②DE⊥AB,③AF=DF.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com