
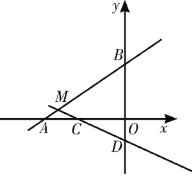
【題目】如圖,在平面直角坐標系xOy中,已知直線AB:y=![]() x+4交x軸于點A,交y軸于點B.直線CD:y=-
x+4交x軸于點A,交y軸于點B.直線CD:y=-![]() x-1與直線AB相交于點M,交x軸于點C,交y軸于點D.
x-1與直線AB相交于點M,交x軸于點C,交y軸于點D.
(1)直接寫出點B和點D的坐標.
(2)若點P是射線MD的一個動點,設點P的橫坐標是x,△PBM的面積是S,求S與x之間的函數關系,并指出x的取值范圍.
(3)當S=10時,平面直角坐標系內是否存在點E,使以點B,E,P,M為頂點的四邊形是平行四邊形?若存在,共有幾個這樣的點?請求出其中一個點的坐標(寫出求解過程);若不存在,請說明理由.
【答案】(1)B(0,4),D(0,-1);(2)![]() (
(![]() );(3)存在,共有3個,E點為(4,
);(3)存在,共有3個,E點為(4,![]() )、(-6,-4)和
)、(-6,-4)和![]()
【解析】
(1)利用y軸上的點的坐標特征即可得出結論.
(2)先求出點M的坐標,再用三角形的面積之和即可得出結論.
(3)分三種情況,根據題意只寫出其中一個求解過程即可,利用對角線互相平分的四邊形是平行四邊形和線段的中點坐標的確定方法即可得出結論.
(1)將x=0代入y=![]() x+4,y=
x+4,y=![]()
![]() +4
+4
解得![]()
將y=0代入y=-![]() x-1,y=-
x-1,y=-![]()
![]() -1
-1
解得![]()
∴B(0,4),D(0,-1)
(2)在解方程組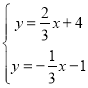
得M點的坐標是![]() ,
,
∵BD=5,
當P點在![]() 軸左側時,如圖(1):
軸左側時,如圖(1):![]() ;
;
當P點在![]() 軸右側時,如圖(2):
軸右側時,如圖(2):![]() .
.
總之,所求的函數關系式是![]() (
(![]() )
)

(3)存在,共有3個.
當S=10時,求得P點為(-1,![]() ),若平行四邊形以MB、MP為鄰邊,如圖,BE∥MD,PE∥MB,可設直線BE的解析式為
),若平行四邊形以MB、MP為鄰邊,如圖,BE∥MD,PE∥MB,可設直線BE的解析式為![]() ,將B點坐標代入得
,將B點坐標代入得![]() ,所以BE的解析式為
,所以BE的解析式為![]() ;同樣可求得PE的解析式為
;同樣可求得PE的解析式為![]() ,解方程組
,解方程組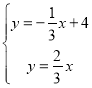
得E點為(4,![]() )
)
[{備注:同理可證另外兩個點,另兩個點的坐標為(-6,-4)和![]() }
}


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:
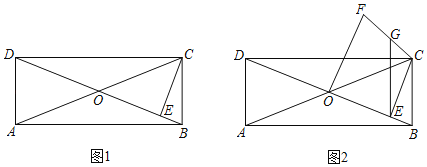
【題目】矩形ABCD的對角線相交于點O,∠COE=45°,過點C作CE⊥BD于點E,
(1)如圖1,若CB=1,求△CED的面積;
(2)如圖2,過點O作OF⊥DB于點O,OF=OD,連接FC,點G是FC中點,連接GE,求證:DC=2GE.
查看答案和解析>>
科目:初中數學 來源: 題型:
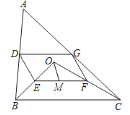
【題目】如圖,點![]() 是ΔABC內一點,連接OB、OC,并將AB、OB、OC、AC的中點
是ΔABC內一點,連接OB、OC,并將AB、OB、OC、AC的中點![]() 、
、![]() 、
、![]() 、
、![]() 依次連結,得到四邊形
依次連結,得到四邊形![]() .
.
(1)求證:四邊形![]() 是平行四邊形;
是平行四邊形;
(2)若![]() 為
為![]() 的中點,OM=5,∠OBC與∠OCB互余,求DG的長度.
的中點,OM=5,∠OBC與∠OCB互余,求DG的長度.
查看答案和解析>>
科目:初中數學 來源: 題型:
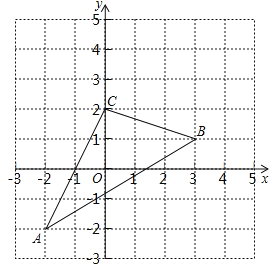
【題目】如圖,△ABC在直角坐標系中.
(1)若把△ABC向上平移2個單位,再向左平移1個單位得到△A1B1C1,畫出△A1B1C1,并寫出點A1,B1,C1的坐標;
(2)求△ABC的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(1)如圖,用尺規作圖的方法作出![]() 的角平分線
的角平分線![]() . (保留作圖痕跡,不要求寫出作法)
. (保留作圖痕跡,不要求寫出作法)
(2)在(1)的基礎上證明命題“全等三角形的對應角角平分線相等”是真命題.請填空并證明.
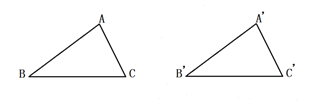
已知:如圖,__________________,![]() 和
和![]() 分別是
分別是![]() 和
和![]() 的平分線.
的平分線.
求證:______________________________.
證明:
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】足球運動員將足球沿與地面成一定角度的方向踢出,足球飛行的路線是一條拋物線,不考慮空氣阻力,足球距離地面的高度![]() (單位:
(單位:![]() )與足球被踢出后經過的時間
)與足球被踢出后經過的時間![]() (單位:
(單位:![]() )之間的關系如下表:
)之間的關系如下表:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | … |
| 0 | 8 | 14 | 18 | 20 | 20 | 18 | 14 | … |
下列結論:①足球距離地面的最大高度為![]() ;②足球飛行路線的對稱軸是直線
;②足球飛行路線的對稱軸是直線![]() ;③足球被踢出
;③足球被踢出![]() 時落地;④足球被踢出
時落地;④足球被踢出![]() 時,距離地面的高度是
時,距離地面的高度是![]() .
.
其中正確結論的個數是( )
A.1 B.2 C.3 D.4
查看答案和解析>>
科目:初中數學 來源: 題型:
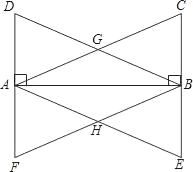
【題目】在Rt△ABC與Rt△ABD中,∠ABC=∠BAD=90°,AC=BD,AC,BD相交于點G,過點A作AE∥DB交CB的延長線于點E,過點B作BF∥CA交DA的延長線于點F,AE,BF相交于點H.
(1)證明:△ABD≌△BAC.
(2)四邊形AHBG是什么樣的四邊形,請猜想并證明.
(3)若使四邊形AHBG是正方形,還需在Rt△ABC添加一個什么條件?請添加條件并證明.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com