
 的
的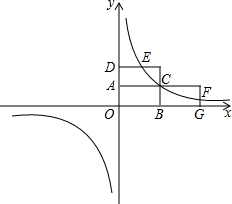 圖象經過點C.
圖象經過點C.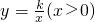 的圖象交于點E、F,求線段EF.
的圖象交于點E、F,求線段EF. 圖象的兩個分支上,請直接寫出線段P、Q兩點的最短距離(不需證明);并利用圖象,求當
圖象的兩個分支上,請直接寫出線段P、Q兩點的最短距離(不需證明);并利用圖象,求當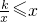 時x的取值范圍.
時x的取值范圍. (k≠0),得2=
(k≠0),得2= ,
, ,
, ,得x=
,得x= ,
, ,4),
,4), ,得y=1,
,得y=1,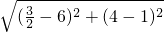 =
=
 ;
;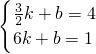 ,
,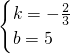 ,
, x+5,
x+5, x+n,
x+n, n,
n, n,0),N(0,n),
n,0),N(0,n), n,ON=n,MN=EF=
n,ON=n,MN=EF=
 ,
, n)2+n2=(
n)2+n2=(
 )2,
)2, x+5上,
x+5上, 中,得:x2=6,
中,得:x2=6, 或-
或- ,
, ,
, ),Q(-
),Q(- ,-
,- ),
),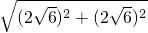 =
= ,
, ≤x時,x的取值范圍為:-
≤x時,x的取值范圍為:- ≤x<0或x≥
≤x<0或x≥ .
. ,-
,- <x<0,0<x<
<x<0,0<x< ,x>
,x> ,找出一次函數y=x在反比例函數圖象上方時x的范圍,即為所求x的范圍.
,找出一次函數y=x在反比例函數圖象上方時x的范圍,即為所求x的范圍.

 天天向上口算本系列答案
天天向上口算本系列答案科目:初中數學 來源: 題型:
 如圖,在平面直角坐標中,四邊形OABC是等腰梯形,CB∥OA,OA=7,AB=4,∠COA=60°,點P為x軸上的一個動點,但是點P不與點0、點A重合.連接CP,D點是線段AB上一點,連接PD.
如圖,在平面直角坐標中,四邊形OABC是等腰梯形,CB∥OA,OA=7,AB=4,∠COA=60°,點P為x軸上的一個動點,但是點P不與點0、點A重合.連接CP,D點是線段AB上一點,連接PD.| BD |
| AB |
| 5 |
| 8 |
查看答案和解析>>
科目:初中數學 來源: 題型:
 (2012•渝北區一模)如圖,在平面直角坐標xoy中,以坐標原點O為圓心,3為半徑畫圓,從此圓內(包括邊界)的所有整數點(橫、縱坐標均為整數)中任意選取一個點,其橫、縱坐標之和為0的概率是
(2012•渝北區一模)如圖,在平面直角坐標xoy中,以坐標原點O為圓心,3為半徑畫圓,從此圓內(包括邊界)的所有整數點(橫、縱坐標均為整數)中任意選取一個點,其橫、縱坐標之和為0的概率是| 5 |
| 29 |
| 5 |
| 29 |
查看答案和解析>>
科目:初中數學 來源: 題型:
 如圖,在平面直角坐標xOy中,已知點A(-5,0),P是反比例函數y=
如圖,在平面直角坐標xOy中,已知點A(-5,0),P是反比例函數y=| k |
| x |
| k |
| x |
查看答案和解析>>
科目:初中數學 來源: 題型:
 ∠COA=45°,動點P從點O出發,在梯形OABC的邊上運動,路徑為O→A→B→C,到達點C時停止.作直線CP.
∠COA=45°,動點P從點O出發,在梯形OABC的邊上運動,路徑為O→A→B→C,到達點C時停止.作直線CP.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com