
【題目】某公司10名銷售員,去年完成的銷售額情況如表:
銷售額(單位:萬元) | 3 | 4 | 5 | 6 | 7 | 8 | 10 |
銷售員人數(單位:人) | 1 | 3 | 2 | 1 | 1 | 1 | 1 |
(1)求銷售額的平均數、眾數、中位數;
(2)今年公司為了調動員工積極性,提高年銷售額,準備采取超額有獎的措施,請根據(1)的結果,通過比較,合理確定今年每個銷售員統一的銷售額標準是多少萬元?
【答案】(1)平均數5.6(萬元);眾數是4(萬元);中位數是5(萬元);(2)今年每個銷售人員統一的銷售標準應是5萬元.
【解析】
(1)根據平均數公式求得平均數,根據次數出現最多的數確定眾數,按從小到大順序排列好后求得中位數.
(2)根據平均數,中位數,眾數的意義回答.
解:
(1)平均數![]() =
=![]() (3×1+4×3+5×2+6×1+7×1+8×1+10×1)=5.6(萬元);
(3×1+4×3+5×2+6×1+7×1+8×1+10×1)=5.6(萬元);
出現次數最多的是4萬元,所以眾數是4(萬元);
因為第五,第六個數均是5萬元,所以中位數是5(萬元).
(2)今年每個銷售人員統一的銷售標準應是5萬元.
理由如下:若規定平均數5.6萬元為標準,則多數人無法或不可能超額完成,會挫傷員工的積極性;若規定眾數4萬元為標準,則大多數人不必努力就可以超額完成,不利于提高年銷售額;若規定中位數5萬元為標準,則大多數人能完成或超額完成,少數人經過努力也能完成.因此把5萬元定為標準比較合理.


 全能測控期末小狀元系列答案
全能測控期末小狀元系列答案科目:初中數學 來源: 題型:
【題目】甲、乙兩人在筆直的湖邊公路上同起點、同終點、同方向勻速步行2400米,先到終點的人原地休息.已知甲先出發4分鐘,在整個步行過程中,甲、乙兩人的距離y(米)與甲出發的時間t(分)之間的關系如圖所示,下列結論:
①甲步行的速度為60米/分;
②乙走完全程用了32分鐘;
③乙用16分鐘追上甲;
④乙到達終點時,甲離終點還有300米
其中正確的結論有( )

A. 1個 B. 2個 C. 3個 D. 4個
查看答案和解析>>
科目:初中數學 來源: 題型:
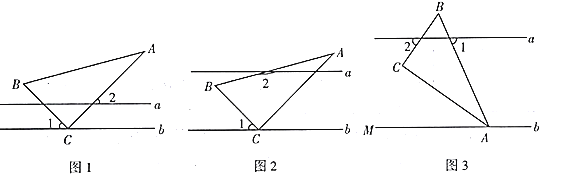
【題目】在綜合與實踐課上,同學們以“一個含![]() 的直角三角尺和兩條平行線”為背景開展數學活動,如圖,已知兩直線
的直角三角尺和兩條平行線”為背景開展數學活動,如圖,已知兩直線![]() 且
且![]() 和直角三角形
和直角三角形![]() ,
,![]() ,
,![]() ,
,![]() .
.
操作發現:
(1)在如圖1中,![]() ,求
,求![]() 的度數;
的度數;
(2)如圖2,創新小組的同學把直線![]() 向上平移,并把
向上平移,并把![]() 的位置改變,發現
的位置改變,發現![]() ,說明理由;
,說明理由;
實踐探究:
(3)縝密小組在創新小組發現結論的基礎上,將如圖中的圖形繼續變化得到如圖,![]() 平分
平分![]() ,此時發現
,此時發現![]() 與
與![]() 又存在新的數量關系,請直接寫出
又存在新的數量關系,請直接寫出![]() 與
與![]() 的數量關系.
的數量關系.
查看答案和解析>>
科目:初中數學 來源: 題型:
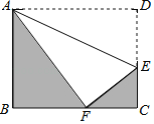
【題目】如圖,將矩形ABCD沿直線AE折疊,頂點D恰好落在BC邊上F點處,已知AD=10cm,BF=6cm.
(1)求DE的值;
(2)求圖中陰影部分的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,在等邊△ABC中,D是BC的中點,P為AB 邊上的一個動點,設AP=x,圖1中線段DP的長為y,若表示y與x的函數關系的圖象如圖2所示,則△ABC的面積為( )
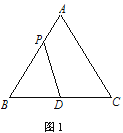
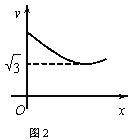
A. 4 B. ![]() C. 12 D.
C. 12 D. ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
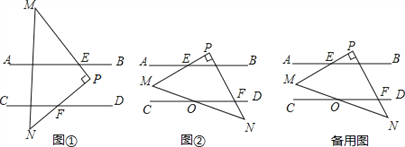
【題目】如圖,已知AB∥CD,現將一直角三角形PMN放入圖中,其中∠P=90°,PM交AB于點E,PN交CD于點F
(1)當△PMN所放位置如圖①所示時,則∠PFD與∠AEM的數量關系為 ;
(2)當△PMN所放位置如圖②所示時,求證:∠PFD﹣∠AEM=90°;
(3)在(2)的條件下,若MN與CD交于點O,且∠DON=30°,∠PEB=15°,求∠N的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
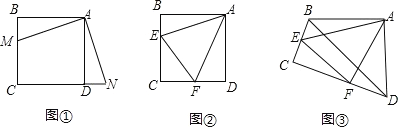
【題目】(1)如圖①,點 M 是正方形 ABCD 的邊 BC 上一點,點 N 是 CD 延長線上一點, 且BM=DN,則線段 AM 與 AN 的關系.
(2)如圖②,在正方形 ABCD 中,點 E、F分別在邊 BC、CD上,且∠EAF=45°,判斷 BE,DF,EF 三條線段的數量關系,并說明理由.
(3)如圖③,在四邊形 ABCD中,AB=AD,∠BAD=90°,∠ABC+∠ADC=180°,點E、F分別在邊 BC、CD 上,且∠EAF=45°,若 BD=5,EF=3,求四邊形 BEFD 的周長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】列方程解應用題:
某玩具廠生產一種玩具,按照控制固定成本降價促銷的原則,使生產的玩具能夠及時售出,據市場調查:每個玩具按![]() 元銷售時,每天可銷售
元銷售時,每天可銷售![]() 個;若銷售單價每降低元,每天可多售出
個;若銷售單價每降低元,每天可多售出![]() 個.已知每個玩具的固定成本為
個.已知每個玩具的固定成本為![]() 元,問這種玩具的銷售單價為多少元時,廠家每天可獲利潤
元,問這種玩具的銷售單價為多少元時,廠家每天可獲利潤![]() 元?
元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系xOy中,已知正比例函數y=![]() x的圖象與反比例函數y=
x的圖象與反比例函數y=![]() 的圖象交于A(a,-2),B兩點.
的圖象交于A(a,-2),B兩點.
(1)求反比例函數的表達式和點B的坐標;
(2)P是第一象限內反比例函數圖象上一點,過點P作y軸的平行線,交直線AB于點C,連接PO,若△POC的面積為3,求點P的坐標.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com