
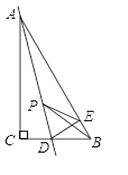
【題目】如圖,在Rt△ABC中,∠C=Rt∠,∠ABC=60°,D是BC邊上的點,CD=1,將△ACD沿直線AD翻折,點C恰好落在直線AB的邊上的E處,若P是直線AD上的動點,則△PEB的周長最小值是____________ .
【答案】![]()
【解析】
根據折疊和等腰三角形性質得出,E關于AD的對稱點為C,即當P和D重合時,PE+BP的值最小,即可此時△BPE的周長最小,最小值是BE+PE+PB=BE+CD+DB=BC+BE,先求出BC和BE長,代入求出即可.
解:∵沿AD折疊C和E重合,
∴∠ACD=∠AED=90°,AC=AE,∠CAD=∠EAD,
∴AD垂直平分CE,即C和E關于AD對稱,CD=DE=1,
∴當P和D重合時,PE+BP的值最小,即此時△BPE的周長最小,最小值是BE+PE+PB=BE+CD+DB=BC+BE,
∵∠DEA=90°,
∴∠DEB=90°,
∵∠ABC=60°,DE=1,
∴BE=![]() ,BD=
,BD=![]() ,即BC=
,即BC=![]() ,
,
∴△PEB的周長的最小值是BC+BE=![]() +
+![]() =
=![]() ,
,
故答案為:![]() .
.


 仁愛英語同步練習冊系列答案
仁愛英語同步練習冊系列答案 學習實踐園地系列答案
學習實踐園地系列答案科目:初中數學 來源: 題型:
【題目】如圖,把一張長方形紙片ABCD沿對角線BD對折,使得點C落在點F處,DF交AB于E,AD=8,AB=16.
(1)求證:DE=BE;
(2)求S△BEF;
(3)若M、N分別為線段CD、DB上的動點,直接寫出(NC+NM)的最小值___________.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知二次函數y=x2+mx+n的圖象經過點P(﹣3,1),對稱軸是直線x=﹣1.
(1)求m,n的值;
(2)x取什么值時,y隨x的增大而減小?
查看答案和解析>>
科目:初中數學 來源: 題型:
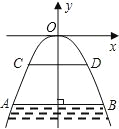
【題目】如圖所示,有一座拋物線形拱橋,橋下面在正常水位時,AB寬20 m,水位上升到警戒線CD時,CD到拱橋頂E的距離僅為1 m,這時水面寬度為10 m.
(1)在如圖所示的坐標系中求拋物線的解析式;
(2)若洪水到來時,水位以每小時0.3 m的速度上升,從正常水位開始,持續多少小時到達警戒線?
查看答案和解析>>
科目:初中數學 來源: 題型:
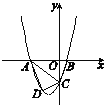
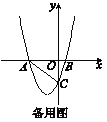
【題目】已知:如圖16,拋物線y=ax2+3ax+c(a>0)與y軸交于點C,與x軸交于A,B兩點,點A在點B左側.點B的坐標為(1,0),OC=3OB.
(1)求拋物線的解析式.
(2)若點D是線段AC下方拋物線上的動點,求四邊形ABCD面積的最大值.
(3)若點E在x軸上,點P在拋物線上.是否存在以A,C,E,P為頂點且以AC為一邊的平行四邊形?若存在,求出點P的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
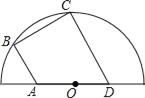
【題目】如圖,四邊形ABCD內接于半圓O,其中點A,D在直徑上,點B,C在半圓弧上,AB∥CD,∠B=90°,若AO=3,∠BAD=120°,則BC=_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】近年來,霧霾天氣給人們的生活帶來很大影響,空氣質量問題倍受人們關注,某學校計劃在教室內安裝空氣凈化裝置,需購進A、B兩種設備,已知:購買1臺A種設備和2臺B種設備需要3.5萬元;購買2臺A種設備和1臺B種設備需要2.5萬元.
(1)求每臺A種、B種設備各多少萬元?
(2)根據學校實際,需購進A種和B種設備共30臺,總費用不超過30萬元,請你通過計算,求至少購買A種設備多少臺?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】根據題意,解答問題:
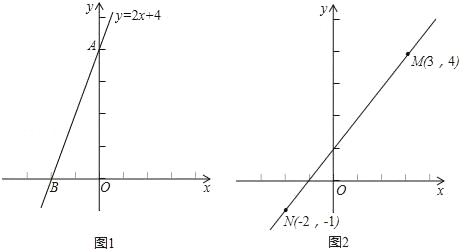
(1)如圖1,已知直線y=2x+4與x軸、y軸分別交于A、B兩點,求線段AB的長.
(2)如圖2,類比(1)的解題過程,請你通過構造直角三角形的方法,求出點M(3,4)與點N(﹣2,﹣1)之間的距離.
(3)在(2)的基礎上,若有一點D在x軸上運動,當滿足DM=DN時,請求出此時點D的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】四邊形ABCD是正方形,E、F分別是DC和CB的延長線上的點,且DE=BF,連接AE、AF、EF.

(1)求證:△ADE≌△ABF;
(2)填空:△ABF可以由△ADE繞旋轉中心 點,按順時針方向旋轉 度得到;
(3)若BC=8,DE=6,求△AEF的面積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com