Question

分別以▱ABCD（∠CDA≠90°）的三邊AB，CD，DA為斜邊作等腰直角三角形，△ABE，△CDG，△ADF．

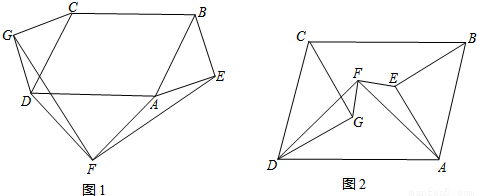
（1）如圖1，當三個等腰直角三角形都在該平行四邊形外部時，連接GF，EF．請判斷GF與EF的關系（只寫結論，不需證明）；

（2）如圖2，當三個等腰直角三角形都在該平行四邊形內部時，連接GF，EF，（1）中結論還成立嗎？若成立，給出證明；若不成立，說明理由．

 

Answer 1

【答案】

解：（1）GF⊥EF，GF=EF。

（2）GF⊥EF，GF=EF成立。理由如下：

∵四邊形ABCD是平行四邊形，∴AB=CD，∠DAB+∠ADC=180°。

∵△ABE，△CDG，△ADF都是等腰直角三角形，

∴DG=CG=AE=BE，DF=AF，∠CDG=∠ADF=∠BAE=45°

∴∠BAE+∠FDA+∠EAF+∠ADF+∠FDC=180°。∴∠EAF+∠CDF=45°。

∵∠CDF+∠GDF=45°，∴∠FDG=∠EAF。

∵在△EAF和△GDF中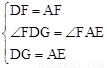，，∴△EAF≌△GDF（SAS）。

∴EF=FG，∠EFA=∠DFG，即∠GFD+∠GFA=∠EFA+∠GFA。

∴∠GFE=90°。∴GF⊥EF。

【解析】

試題分析：（1）根據等腰直角三角形的性質以及平行四邊形的性質得出∠FDG=∠EAF，進而得出△EAF≌△GDF即可得出答案：

∵四邊形ABCD是平行四邊形，∴AB=CD，∠DAB+∠ADC=180°。

∵△ABE，△CDG，△ADF都是等腰直角三角形，

∴DG=CG=AE=BE，DF=AF，∠CDG=∠ADF=∠BAE=45°。

∴∠GDF=∠GDC+∠CDA+∠ADF=90°+∠CDA，

∠EAF=360°﹣∠BAE﹣∠DAF﹣∠BAD=270°﹣（180°﹣∠CDA）=90°+∠CDA。

∴∠FDG=∠EAF。

∵在△EAF和△GDF中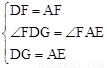，，∴△EAF≌△GDF（SAS）。

∴EF=FG，∠EFA=∠DFG，即∠GFD+∠GFA=∠EFA+∠GFA。

∴∠GFE=90°。∴GF⊥EF。

（2）根據等腰直角三角形的性質以及平行四邊形的性質得出∠FDG=∠EAF，進而得出△EAF≌△GDF即可得出答案。