
【題目】已知平面直角坐標系中兩定點A(﹣1,0)、B(4,0),拋物線y=ax2+bx﹣2(a≠0)過點A,B,頂點為C,點P(m,n)(n<0)為拋物線上一點.
(1)求拋物線的解析式和頂點C的坐標;
(2)當∠APB為鈍角時,求m的取值范圍;
(3)若m>![]() ,當∠APB為直角時,將該拋物線向左或向右平移t(0<t<
,當∠APB為直角時,將該拋物線向左或向右平移t(0<t<![]() )個單位,點C、P平移后對應的點分別記為C′、P′,是否存在t,使得首位依次連接A、B、P′、C′所構成的多邊形的周長最短?若存在,求t的值并說明拋物線平移的方向;若不存在,請說明理由.
)個單位,點C、P平移后對應的點分別記為C′、P′,是否存在t,使得首位依次連接A、B、P′、C′所構成的多邊形的周長最短?若存在,求t的值并說明拋物線平移的方向;若不存在,請說明理由.
【答案】(1) 拋物線的解析式為:y=![]() x2﹣
x2﹣![]() x﹣2;C(
x﹣2;C( ![]() ,﹣
,﹣![]() ).(2) ﹣1<m<0或3<m<4;(3)
).(2) ﹣1<m<0或3<m<4;(3)![]()
【解析】分析:(1)待定系數法求解析式即可,求得解析式后轉換成頂點式即可.
(2)因為AB為直徑,所以當拋物線上的點P在⊙C的內部時,滿足∠APB為鈍角,所以-1<m<0,或3<m<4.
(3)左右平移時,使A′D+DB″最短即可,那么作出點C′關于x軸對稱點的坐標為C″,得到直線P″C″的解析式,然后把A點的坐標代入即可.
詳解:(1)∵拋物線y=ax2+bx﹣2(a≠0)過點A,B,
∴![]() ,
,
解得: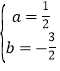 ,
,
∴拋物線的解析式為:y=![]() x2﹣
x2﹣![]() x﹣2;
x﹣2;
∵y=![]() x2﹣
x2﹣![]() x﹣2=
x﹣2=![]() (x﹣
(x﹣![]() )2﹣
)2﹣![]() ,
,
∴C(![]() ,﹣
,﹣![]() ).
).
(2)如圖1,以AB為直徑作圓M,則拋物線在圓內的部分,能使∠APB為鈍角,
∴M(![]() ,0),⊙M的半徑=
,0),⊙M的半徑=![]() .
.
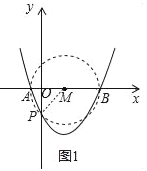
∵P′是拋物線與y軸的交點,
∴OP′=2,
∴MP′=![]() ,
,
∴P′在⊙M上,
∴P′的對稱點(3,﹣2),
∴當﹣1<m<0或3<m<4時,∠APB為鈍角.
(3)存在;
拋物線向左或向右平移,因為AB、P′C′是定值,所以A、B、P′、C′所構成的多邊形的周長最短,只要AC′+BP′最小;
第一種情況:拋物線向右平移,AC′+BP′>AC+BP,
第二種情況:向左平移,如圖2所示,由(2)可知P(3,﹣2),
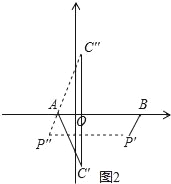
又∵C(![]() ,﹣
,﹣![]() )
)
∴C'(![]() ﹣t,﹣
﹣t,﹣![]() ),P'(3﹣t,﹣2),
),P'(3﹣t,﹣2),
∵AB=5,
∴P″(﹣2﹣t,﹣2),
要使AC′+BP′最短,只要AC′+AP″最短即可,
點C′關于x軸的對稱點C″(![]() ﹣t,
﹣t,![]() ),
),
設直線P″C″的解析式為:y=kx+b,
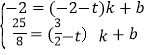 ,
,
解得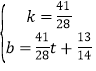
∴直線y=![]() ,
,
當P″、A、C″在一條直線上時,周長最小,
∴![]() =0
=0
∴t=![]() .
.
故將拋物線向左平移![]() 個單位連接A、B、P′、C′所構成的多邊形的周長最短.
個單位連接A、B、P′、C′所構成的多邊形的周長最短.


科目:初中數學 來源: 題型:
【題目】如圖,已知直線l:y=ax+b與反比例函數y=﹣![]() 的圖象交于A(﹣4,1)、B(m,﹣4),且直線l與y軸交于點C.
的圖象交于A(﹣4,1)、B(m,﹣4),且直線l與y軸交于點C.
(1)求直線l的解析式;
(2)若不等式ax+b>﹣![]() 成立,則x的取值范圍是 ;
成立,則x的取值范圍是 ;
(3)若直線x=n(n<0)與y軸平行,且與雙曲線交于點D,與直線l交于點H,連接OD、OH、OA,當△ODH的面積是△OAC面積的一半時,求n的值.

查看答案和解析>>
科目:初中數學 來源: 題型:
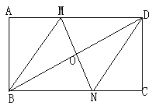
【題目】如圖,在矩形ABCD中,對角線BD的垂直平分線MN與AD相交于點N,連接BM,DN.
(1)求證:四邊形BMDN是菱形;
(2)若AB=4,AD=8,求MD的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:如圖,在梯形ABCD中,AB∥CD,∠D=90°,AD=CD=2,點E在邊AD上(不與點A、D重合),∠CEB=45°,EB與對角線AC相交于點F,設DE=x.
(1)用含x的代數式表示線段CF的長;
(2)如果把△CAE的周長記作C△CAE,△BAF的周長記作C△BAF,設![]() =y,求y關于x的函數關系式,并寫出它的定義域;
=y,求y關于x的函數關系式,并寫出它的定義域;
(3)當∠ABE的正切值是![]() 時,求AB的長.
時,求AB的長.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知∠AOB=90°,∠BOC=30°,OM平分∠AOC,ON平分∠BOC.
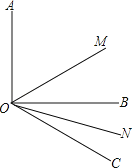
(1)求∠MON的度數;
(2)如果∠AOB=α,其他條件不變,求∠MON的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
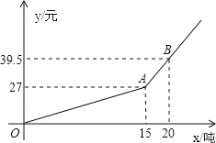
【題目】某市自來水公司為鼓勵居民節約用水,采取按月用水量分段收費辦法,若某戶居民應交交費![]() (元)與用水量
(元)與用水量![]() (噸)的函數關系如圖所示。
(噸)的函數關系如圖所示。
(1)分別寫出當![]() 和
和![]() 時,
時,![]() 與
與![]() 的函數關系式;
的函數關系式;
(2)若某用戶該月用水21噸,則應交水費多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,正方形ABCD中,G為BC邊上一點,BE⊥AG于E,DF⊥AG于F,連接DE.
(1)求證:△ABE≌△DAF;
(2)若AF=1,四邊形ABED的面積為6,求EF的長.

查看答案和解析>>
科目:初中數學 來源: 題型:
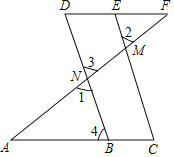
【題目】如圖,∠1=∠2,∠A=∠F,求證:∠C=∠D.請閱讀下面的解答過程,并填空(理由或數學式)
證明:∵∠1=∠2(已知)∠1=∠3(_______)
∴∠2=∠3(等量代換)
∴BD∥_____(_______)
∴∠4=_____(_______)
又∵∠A=∠F(已知)
∴AC∥_____(_______)
∴∠4=_____(_______)
∴∠C=∠D(等量代換)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com