【題目】如圖，已知△ABC中，高為AD，角平分線為AE，若∠B=28°，∠ACD=52°，求∠EAD的度數． 
【答案】解：在△ABC中，∵∠ACD=∠B+∠BAC，
∴∠BAC=52°﹣28°=24°，
∵AE平分∠BAC，
∴∠BAE= 
∠BAC=12°，
∴∠AED=∠B+∠BAE=28°+12°=40°，
∵AD為高，
∴∠ADE=90°，
∴∠EAD=90°﹣∠AED=90°﹣40°=50°
【解析】先根據三角形外角性質計算出∠BAC=24°，再根據角角平分線定義得到∠BAE= 
∠BAC=12°，接著再利用三角形外角性質得到∠AED=∠B+∠BAE=40°，然后根據互余計算出∠EAD的度數．
【考點精析】根據題目的已知條件，利用三角形的內角和外角的相關知識可以得到問題的答案，需要掌握三角形的三個內角中，只可能有一個內角是直角或鈍角；直角三角形的兩個銳角互余；三角形的一個外角等于和它不相鄰的兩個內角的和；三角形的一個外角大于任何一個和它不相鄰的內角．
能力評價系列答案
唐印文化課時測評系列答案
導學與測試系列答案科目：初中數學 來源： 題型：
【題目】為了節約用水，某市決定調整居民用水收費方法，規定：
①如果每戶每月水不超過
噸，每噸水收費
元．
②如果每戶每月用水超過
噸，則超過部分每噸水收費
元．
小紅看到這種收費方法后，想算算她家每月的水費，但是她不清楚家里每月的用水是否超過
噸．
（
）如果小紅家每月用水
噸，水費是多少？如果每月用水
噸，水費是多少？
（
）如果字母
表示小紅家每月用水的噸數，那么小紅家每月的水費該如何用
的代數式表示呢？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在△ABC中，點D為BC上一點，過A，B，D三點作⊙O，AE是⊙O的直徑，AC是⊙O的切線，AD=DC，連結DE．
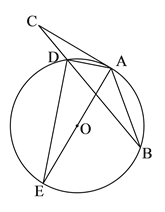
（1）求證：AB=AC；
（2）若
，AC=
，求△ADE的周長.
查看答案和解析>>
科目：初中數學 來源： 題型：
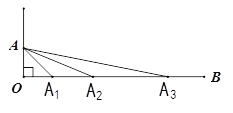
【題目】如圖，已知
，點
繞點
順時針旋轉后的對應點
落在射線
上，點
繞點
順時針旋轉后的對應點
落在射線
上，點
繞點
順時針旋轉后的對應點
落在射線
上，…，連接
、
、
…，以此作法，則
=______度．（用含
的代數式表示， 
為正整數）
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在等邊△ABC中，點F是AC邊上一點，延長BC到點D，使BF=DF，若CD=CF，求證：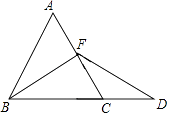 
（1）點F為AC的中點；
（2）過點F作FE⊥BD，垂足為點E，請畫出圖形并證明BD=6CE．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
