
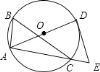
【題目】如圖,![]() 內接于
內接于![]() ,
,![]() ,
,![]() 是直徑,過點
是直徑,過點![]() 作
作![]() 的切線交
的切線交![]() 的延長線于
的延長線于![]() ,如果
,如果![]() ,
,![]() ,則
,則![]() ________.
________.
【答案】![]()
【解析】
連DC,過A點作AF⊥BC,由∠B=60°,得∠ADC=60°,再由AD為直徑,DE為⊙O的切線,可得∠ADE=90°,∠DCE=90°,∠DAE=30°,
由CE=![]() ,利用含30度的直角三角形的三邊的關系即可求得DC=
,利用含30度的直角三角形的三邊的關系即可求得DC=![]() EC=
EC=![]() ×
×![]() =
=![]() ,AD=2
,AD=2![]() ,AC=
,AC=![]() ×
×![]() =
=![]() ,而AB=2,由此可得到△OAB為等腰直角三角形,則∠AOB=90°,∠ACB=45°;在Rt△ACF中,AC=
,而AB=2,由此可得到△OAB為等腰直角三角形,則∠AOB=90°,∠ACB=45°;在Rt△ACF中,AC=![]() CF,所以CF=
CF,所以CF=![]() ×
×![]() =
=![]() ,在Rt△ABF中,AB=2BF,所以BF=
,在Rt△ABF中,AB=2BF,所以BF=![]() ×2=1,于是得到BC的長.
×2=1,于是得到BC的長.
連DC,OB,過A點作AF⊥BC,如圖,
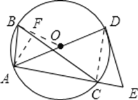
∵∠B=60°,
∴∠ADC=60°,
又∵DE為⊙O的切線,
∴∠ADE=90°,
而AD為直徑,
∴∠DCE=90°,則∠DAE=30°,
∵CE=![]() ,
,
∴DC=![]() EC=
EC=![]() ×
×![]() =
=![]() ,
,
∴在Rt△ADC中,AD=2![]() ,AC=
,AC=![]() ×
×![]() =
=![]() ,
,
在△OAB中,OB=OA=![]() ,AB=2,所以△OAB為等腰直角三角形,
,AB=2,所以△OAB為等腰直角三角形,
∴∠AOB=90°,
∴∠ACB=45°,
在Rt△ACF中,AC=![]() CF,所以CF=
CF,所以CF=![]() ×
×![]() =
=![]() ,
,
在Rt△ABF中,AB=2BF,所以BF=![]() ×2=1,
×2=1,
所以BC=BF+FC=![]() +1.
+1.
故答案為1+![]() .
.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
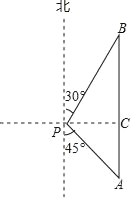
【題目】隨著航母編隊的成立,我國海軍日益強大,2018年4月12日,中央軍委在南海海域降重舉行海上閱兵,在閱兵之前我軍加強了海上巡邏,如圖,我軍巡邏艦在某海域航行到A處時,該艦在觀測點P的南偏東45°的方向上,且與觀測點P的距離PA為400海里;巡邏艦繼續沿正北方向航行一段時間后,到達位于觀測點P的北偏東30°方向上的B處,問此時巡邏艦與觀測點P的距離PB為多少海里?(參考數據:![]() ≈1.414,
≈1.414,![]() ≈1.732,結果精確到1海里).
≈1.732,結果精確到1海里).
查看答案和解析>>
科目:初中數學 來源: 題型:
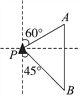
【題目】如圖,一艘海輪位于燈塔P的北偏東60°方向,距離燈塔86 n mile的A處,它沿正南方向航行一段時間后,到達位于燈塔P的南偏東45°方向上的B處,此時B處與燈塔P的距離約為_______nmile.(結果取整數,參考數據:![]() =1.7,
=1.7, ![]() ≈ 1.4)
≈ 1.4)
查看答案和解析>>
科目:初中數學 來源: 題型:
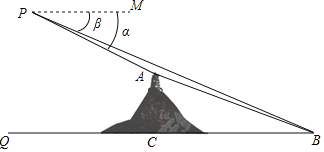
【題目】數學實踐活動小組借助載有測角儀的無人機測量象山嵐光閣與文明湖湖心亭之間的距離.如圖,無人機所在位置P與嵐光閣閣頂A、湖心亭B在同一鉛垂面內,P與B的垂直距離為300米,A與B的垂直距離為150米,在P處測得A、B兩點的俯角分別為α、β,且tanα=![]() ,tanβ=
,tanβ=![]() ﹣1,試求嵐光閣與湖心亭之間的距離AB.(計算結果若含有根號,請保留根號)
﹣1,試求嵐光閣與湖心亭之間的距離AB.(計算結果若含有根號,請保留根號)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,甲樓樓高![]() 米,乙樓座落在甲樓的正北面,已知當地冬至中午
米,乙樓座落在甲樓的正北面,已知當地冬至中午![]() 時太陽光線與水平面的夾角為
時太陽光線與水平面的夾角為![]() ,此時求:
,此時求:
①如果兩樓相距![]() 米,那么甲樓的影子落在乙樓上有多高?________
米,那么甲樓的影子落在乙樓上有多高?________
②如果甲樓的影子剛好不落在乙樓上,那么兩樓的距離應當是________米.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖![]() ,一架
,一架![]() 米長的梯子
米長的梯子![]() 斜靠在與地面
斜靠在與地面![]() 垂直的墻
垂直的墻![]() 上,梯子
上,梯子![]() 與地面
與地面![]() 的傾斜角
的傾斜角![]() 為
為![]() .
.
![]() 求
求![]() 與
與![]() 的長;
的長;
![]() 若梯子頂端
若梯子頂端![]() 沿
沿![]() 下滑,如圖
下滑,如圖![]() ,設
,設![]() 點下滑至
點下滑至![]() 點,
點,![]() 點向右滑行至
點向右滑行至![]() 點.若
點.若![]() ,試求梯子頂端
,試求梯子頂端![]() 沿
沿![]() 下滑多少米;
下滑多少米;
![]() 若梯子頂端
若梯子頂端![]() 沿
沿![]() 下滑,如圖
下滑,如圖![]() ,設
,設![]() 點下滑至
點下滑至![]() 點,
點,![]() 點向右滑行至
點向右滑行至![]() 點,梯子
點,梯子![]() 的中點
的中點![]() ,也隨之運動到點
,也隨之運動到點![]() ,若
,若![]() ,試求
,試求![]() 的長.
的長.

查看答案和解析>>
科目:初中數學 來源: 題型:
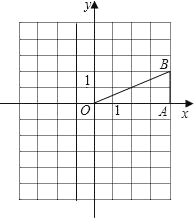
【題目】如圖,在平面直角坐標系中,已知點B(4,2),BA⊥x軸于A.
(1)畫出將△OAB繞原點順時針旋轉90°后所得的△OA1B1,并寫出點A1、B1的坐標;
(2)畫出△OAB關于原點O的中心對稱圖形△OA2B2,并寫出點A2、B2的坐標.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com