
閱讀下列材料并解答。
例 平面上有n個點(n≥2)且任意三個點不在同一條直線上,過這些點作直線,一共能作出多少條不同的直線?
(1)分析:當僅有兩個點時,可連成1條直線;當有3個點時,可連成3條直線;當有4個點時,可連成6條直線;當有5個點時,可連成10條直線……
(2)歸納:考察點的個數和可連成直線的條數![]() 發現:如下表
發現:如下表
| 點的個數 | 可作出直線條數 |
| 2 | 1= |
| 3 | 3= |
| 4 | 6= |
| 5 | 10= |
| …… | …… |
| n |
|
(3)推理:平面上有n個點,兩點確定一條直線。取第一個點A有n種取法,取第二個點B有(n-1)種取法,所以一共可連成n(n-1)條直線,但AB與BA是同一條直線,
故應除以2;即![]()
(4)![]() 結論:
結論:![]()
![]()
試探究以下幾個問題:
平面上有n個點(n≥3),任意三個點不在同一條直線上,過任意三個點作三角形,一共能作出多少不同的三角形?
(1)分析:
當僅有3個點時,可作出 個三角形;
當僅有4個點時,可作出 個三角形;
當僅有5個點時,可作出 個三角形;
……
(2)歸納:考察點的個數n和可作出的三角形的個數![]() ,發現:(填下表)
,發現:(填下表)
| 點的 | 可連成三角形個數 |
| 3 | |
| 4 | |
| 5 | |
| …… | |
| n |
( 3 ) 推理:
(4)結論:
科目:初中數學 來源: 題型:閱讀理解
| 1 |
| a |
| 1 |
| a2 |
查看答案和解析>>
科目:初中數學 來源:2011-2012學年遼寧丹東七中八年級下期期中考試數學試卷(帶解析) 題型:解答題
閱讀下列材料,并解答后面的問題:
∵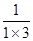 =
=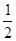 (1-
(1-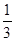 ),
), 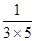 =
=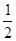 (
(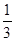 -
-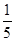 ), … ,
), … ,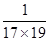 =
=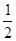 (
(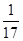 -
-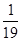 )
)
∴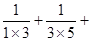 ……+
……+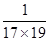
=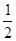 (1-
(1-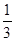 )+
)+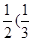 -
-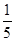 )+ … +
)+ … +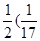 -
-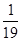 )
)
=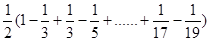
=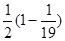
=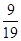
①在式子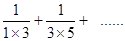 中,第五項為 ,第n項為 。
中,第五項為 ,第n項為 。
②解方程: =
=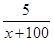 (有計算過程)
(有計算過程)
查看答案和解析>>
科目:初中數學 來源:2013屆遼寧丹東七中八年級下期期中考試數學試卷(解析版) 題型:解答題
閱讀下列材料,并解答后面的問題:
∵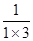 =
=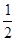 (1-
(1-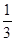 ),
), 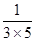 =
=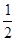 (
(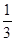 -
-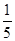 ), … ,
), … ,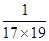 =
=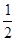 (
(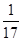 -
-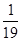 )
)
∴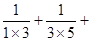 ……+
……+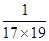
=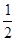 (1-
(1-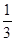 )+
)+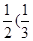 -
-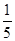 )+ … +
)+ … +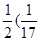 -
-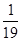 )
)
=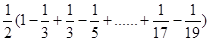
=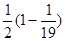
=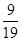
①在式子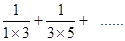 中,第五項為 ,第n項為
。
中,第五項為 ,第n項為
。
②解方程: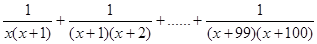 =
=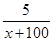 (有計算過程)
(有計算過程)
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 =6,則a2+
=6,則a2+ =______;
=______;查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com