
【題目】如圖,在直角梯形ABCD中,AD∥BC,∠B=90°,且AD=12cm,AB=8cm,DC=10cm,若動點P從A點出發,以每秒2cm的速度沿線段AD向點D運動;動點Q從C點出發以每秒3cm的速度沿CB向B點運動,當P點到達D點時,動點P、Q同時停止運動,設點P、Q同時出發,并運動了t秒,回答下列問題:
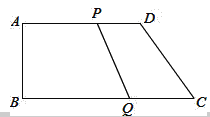
(1)BC= cm;
(2)當t為多少時,四邊形PQCD成為平行四邊形?
(3)當t為多少時,四邊形PQCD為等腰梯形?
(4)是否存在t,使得△DQC是等腰三角形?若存在,請求出t的值;若不存在,說明理由.
【答案】(1)18;(2)當t=![]() 秒時四邊形PQCD為平行四邊形;(3)當t=
秒時四邊形PQCD為平行四邊形;(3)當t=![]() 時,四邊形PQCD為等腰梯形;(4)存在t, t的值為
時,四邊形PQCD為等腰梯形;(4)存在t, t的值為![]() 秒或4秒或
秒或4秒或![]() 秒.
秒.
【解析】試題分析:(1)作DE⊥BC于E,則四邊形ABED為矩形.在直角△CDE中,已知DC、DE的長,根據勾股定理可以計算EC的長度,根據BC=BE+EC即可求出BC的長度;
(2)由于PD∥QC,所以當PD=QC時,四邊形PQCD為平行四邊形,根據PD=QC列出關于t的方程,解方程即可;
(3)首先過D作DE⊥BC于E,可求得EC的長,又由當PQ=CD時,四邊形PQCD為等腰梯形,可求得當QC-PD=QC-EF=QF+EC=2CE,即3t-(12-2t)=12時,四邊形PQCD為等腰梯形,解此方程即可求得答案;
(4)因為三邊中,每兩條邊都有相等的可能,所以應考慮三種情況.結合路程=速度×時間求得其中的有關的邊,運用等腰三角形的性質和解直角三角形的知識求解.
試題解析:根據題意得:PA=2t,CQ=3t,則PD=AD-PA=12-2t.
(1)如圖,過D點作DE⊥BC于E,則四邊形ABED為矩形,
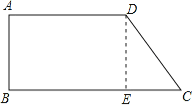
DE=AB=8cm,AD=BE=12cm,
在直角△CDE中,∵∠CED=90°,DC=10cm,DE=8cm,
∴EC=![]() =6cm,
=6cm,
∴BC=BE+EC=18cm.
(2)∵AD∥BC,即PD∥CQ,
∴當PD=CQ時,四邊形PQCD為平行四邊形,
即12-2t=3t,
解得t=![]() 秒,
秒,
故當t=![]() 秒時四邊形PQCD為平行四邊形;
秒時四邊形PQCD為平行四邊形;
(3)如圖,過D點作DE⊥BC于E,則四邊形ABED為矩形,DE=AB=8cm,AD=BE=12cm,
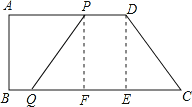
當PQ=CD時,四邊形PQCD為等腰梯形.
過點P作PF⊥BC于點F,過點D作DE⊥BC于點E,則四邊形PDEF是矩形,EF=PD=12-2t,PF=DE.
在Rt△PQF和Rt△CDE中,
![]() ,
,
∴Rt△PQF≌Rt△CDE(HL),
∴QF=CE,
∴QC-PD=QC-EF=QF+EC=2CE,
即3t-(12-2t)=12,
解得:t=![]() ,
,
即當t=![]() 時,四邊形PQCD為等腰梯形;
時,四邊形PQCD為等腰梯形;
(4)△DQC是等腰三角形時,分三種情況討論:
①當QC=DC時,即3t=10,
∴t=![]() ;
;
②當DQ=DC時, ![]()
∴t=4;
③當QD=QC時,3t×![]()
∴t=![]() .
.
故存在t,使得△DQC是等腰三角形,此時t的值為![]() 秒或4秒或
秒或4秒或![]() 秒.
秒.


科目:初中數學 來源: 題型:
【題目】在△ABC中,點D在邊BA或BA的延長線上,過點D作DE∥BC,交∠ABC的角平分線于點E.
(1)如圖1,當點D在邊BA上時,點E恰好在邊AC上,求證:∠ADE=2∠DEB;
(2)如圖2,當點D在BA的延長線上時,請直接寫出∠ADE與∠DEB之間的數量關系,并說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某部隊要進行一次急行軍訓練,路程為32km.大部隊先行,出發1小時后,由特種兵組成的突擊小隊才出發,結果比大部隊提前20分鐘到達目的地.已知突擊小隊的行進速度是大部隊的1.5倍.
(1)求大部隊的行進速度.(列方程解應用題)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某次考試中,某班級的數學成績統計圖如下.下列說法錯誤的是( )

A. 得分在70~80分之間的人數最多
B. 該班的總人數為40
C. 得分在90~100分之間的人數最少
D. 及格(≥60分)人數是26
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在每個小正方形的邊長均為1的7×7網格圖中,格點上有A,B,C,D,E五個定點,如圖所示,一個動點P從點E出發,繞點A逆時針旋轉90°,之后該動點繼續繞點B,C,D逆時針90°后回到初始位置,點P運轉路線的總長是 . (結果保留π)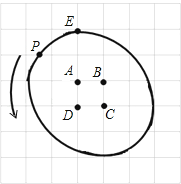
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,點B、E、C、F在一條直線上,AB = DF,AC = DE,BE = CF.
求證: (1) △ABC ≌ △DFE ;
(2)連接AF、BD,求證:四邊形ABDF是平行四邊形.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AD是BC邊上的中線,E是AD的中點,過點A作BC的平行線交BE的延長線于點F,連接CF.
(1)求證:AF=DC ;
(2)若∠BAC=![]() ,試判斷四邊形ADCF的形狀,并證明你的結論.
,試判斷四邊形ADCF的形狀,并證明你的結論.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】 如圖,△ABC的周長是32,以它的三邊中點為頂點組成第2個三角形,再以第2個三角形的三邊中點為頂點組成的第3個三角形,…,則第n個三角形的周長為 . 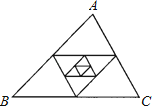
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】建設銀行的某儲蓄員小張在辦理業務時,約定存入為正,取出為負.![]() 年
年![]() 月
月![]() 日他辦理了
日他辦理了![]() 件業務:
件業務:![]() 元、
元、![]() 元、
元、![]() 元、
元、![]() 元、
元、![]() 元、
元、![]() 元.
元.
![]() 若他早上領取備用金
若他早上領取備用金![]() 元,那么下班時應交回銀行多少元?
元,那么下班時應交回銀行多少元?
![]() 若每辦一件業務,銀行發給業務量的
若每辦一件業務,銀行發給業務量的![]() 作為獎勵,那么這天小張應得獎金多少元?
作為獎勵,那么這天小張應得獎金多少元?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com