
【題目】如圖1,P為∠MON平分線OC上一點,以P為頂點的∠APB兩邊分別與射線OM和ON交于A. B兩點,如果∠APB在繞點P旋轉時始終滿足OAOB=OP![]() ,我們就把∠APB叫做∠MON的關聯角.
,我們就把∠APB叫做∠MON的關聯角.
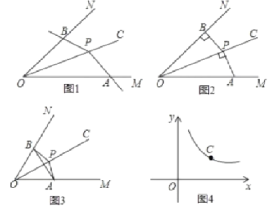
(1)如圖2,P為∠MON平分線OC上一點,過P作PB⊥ON于B,AP⊥OC于P,那么∠APB___∠MON的關聯角(填“是”或“不是”).
(2)①如圖3,如果∠MON=60°,OP=2,∠APB是∠MON的關聯角,連接AB,求△AOB的面積和∠APB的度數;
②如果∠MON=α°(0°<α°<90°),OP=m,∠APB是∠MON的關聯角,直接用含有α和m的代數式表示△AOB的面積。
(3)如圖4,點C是函數y=![]() (x>0)圖象上一個動點,過點C的直線CD分別交x軸和y軸于A,B兩點,且滿足BC=2CA,直接寫出∠AOB的關聯角∠APB的頂點P的坐標。
(x>0)圖象上一個動點,過點C的直線CD分別交x軸和y軸于A,B兩點,且滿足BC=2CA,直接寫出∠AOB的關聯角∠APB的頂點P的坐標。
【答案】(1) 是;(2)①![]() ,150°;②
,150°;②![]() m×sinα;(3) 點(
m×sinα;(3) 點(![]() ,
,![]() )或(
)或(![]() ,
,![]() )或(
)或(![]() ,
,![]() ),P2(
),P2(![]() ,
,![]() ).
).
【解析】
(1)先判斷出△OBP∽△OPA,即可;
(2)①先根據關聯角求出OA×OB=4,再利用三角形的面積公式,以及相似,得到∠OAP=∠OPB,即可;②根據三角形面積公式把α和m代入即可;
(3)根據條件分情況討論,點B在y軸正半軸和負半軸,在負半軸時,經過計算,不存在,②在正半軸時,由BC=2AC判斷出點C是線段AB的一個三等分點,即可.
(1)∵P為∠MON平分線OC上一點,
∴∠BOP=∠AOP,
∵PB⊥ON于B,AP⊥OC于P,
∴∠OBP=∠OPA,
∴△OBP∽△OPA,
∴![]() ,
,
∴OP![]() =OA×OB,
=OA×OB,
∴∠APB是∠MON的關聯角.
故答案為是.
(2)①如圖,過點A作AH⊥OB,
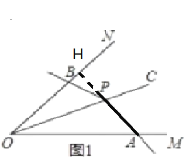
∵∠APB是∠MON的關聯角,OP=2,
∴OA×OB=OP![]() =4,
=4,
在Rt△AOH中,∠AOH=90°,
∴sin∠AOH=![]() ,
,
∴AH=OAsin∠AOH,
∴S![]() =
=![]() OB×AH=
OB×AH=![]() OB×OA×sin60°=
OB×OA×sin60°=![]() ×OP
×OP×
![]() =
=![]() ,
,
∵OP![]() =OA×OB,
=OA×OB,
∴![]() ,
,
∵點P為∠MON的平分線上一點,
∴∠AOP=∠BOP=![]() ∠MON=30°,
∠MON=30°,
∴△AOP∽△POB,
∴∠OAP=∠OPB,
∴∠APB=∠OPB+∠OPA=∠OAP+∠OPA=180°30°=150°,
②由①有,S![]() =
=![]() OB×OA×∠MON=
OB×OA×∠MON=![]() m×sinα;
m×sinα;
(3)∵過點C的直線CD分別交x軸和y軸于A,B兩點,且滿足BC=2CA,
∴只有點A在x軸正半軸,
①當點B在y軸負半軸時,設A(m,0),B(0,n)(m>0,n<0)
∴OA=m,OB=n,
∵BC=2CA,
∴點A是BC中點,
∴點C(2m,n),
∵點C在雙曲線y=2x上,
∴2m×(n)=2,
∴mn=1(不符合題意,舍去),
∵∠AOB的關聯角∠APB
∴OP![]() =OA×0B=|m||n|=1,
=OA×0B=|m||n|=1,
∴OP=1,
∵點P在∠AOB的平分線上,設P(a,a),
∴OP![]() =2a
=2a![]() ,
,
∴2a![]() =1,
=1,
∴a=±![]() ,
,
∴點P(![]() ,
,![]() )或(
)或(![]() ,
,![]() )
)
②當點B在y軸正半軸,設A(m,0),B(0,n)(m>0,n>0)
∴點C(![]() ),
),
∴=2,
∴mn=9,
∵∠AOB的關聯角∠APB
∴OP![]() =OA×0B=mn=9,
=OA×0B=mn=9,
∴OP=3,
∵點P在∠AOB的平分線上,設P(a,a),
∴OP![]() =2a
=2a![]() ,
,
∴2a![]() =9,
=9,
∴a=±![]() ,
,
即:點P![]() (
(![]() ,
,![]() ),P2(
),P2(![]() ,
,![]() ),
),
綜上所述,點(![]() ,
,![]() )或(
)或(![]() ,
,![]() )或(
)或(![]() ,
,![]() ),P2(
),P2(![]() ,
,![]() ).
).


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
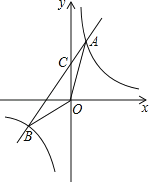
【題目】如圖,已知一次函數y=kx+b的圖象與反比例函數y=![]() 的圖象交于A,B兩點,點A的橫坐標是2,點B的縱坐標是-2.
的圖象交于A,B兩點,點A的橫坐標是2,點B的縱坐標是-2.
(1)求一次函數的解析式;
(2)求△AOB的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,拋物線y=ax2+bx﹣3(a≠0)與x軸交于點A(﹣2,0)、B(4,0)兩點,與y軸交于點C.
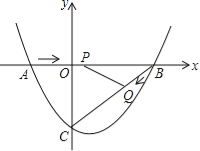
(1)求拋物線的解析式;
(2)點P從A點出發,在線段AB上以每秒3個單位長度的速度向B點運動,同時點Q從B點出發,在線段BC上以每秒1個單位長度的速度向C點運動,其中一個點到達終點時,另一個點也停止運動,當△PBQ存在時,求運動多少秒使△PBQ的面積最大,最大面積是多少?
(3)當△PBQ的面積最大時,在BC下方的拋物線上存在點K,使S△CBK:S△PBQ=5:2,求K點坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系中,對于點P(x,y)和Q(x,y′),給出如下定義:如果y′=![]() ,那么稱點Q為點P的“伴隨點”.
,那么稱點Q為點P的“伴隨點”.
例如:點(5,6)的“伴隨點”為點(5,6);點(﹣5,6)的“伴隨點”為點(﹣5,﹣6).
(1)直接寫出點A(2,1)的“伴隨點”A′的坐標.
(2)點B(m,m+1)在函數y=kx+3的圖象上,若其“伴隨點”B′的縱坐標為2,求函數y=kx+3的解析式.
(3)點C、D在函數y=﹣x2+4的圖象上,且點C、D關于y軸對稱,點D的“伴隨點”為D′.若點C在第一象限,且CD=DD′,求此時“伴隨點”D′的橫坐標.
(4)點E在函數y=﹣x2+n(﹣1≤x≤2)的圖象上,若其“伴隨點”E′的縱坐標y′的最大值為m(1≤m≤3),直接寫出實數n的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
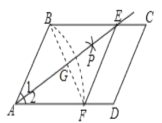
【題目】如圖,在平行四邊形ABCD中,以點A為圓心,AB長為半徑畫弧交AD于點F,再分別以點B. F為圓心,大于![]() BF的相同長度為半徑畫弧,兩弧交于點P;連接AP并延長交BC于點E,連接EF.若四邊形ABEF的周長為16,∠C=60°,AG=2
BF的相同長度為半徑畫弧,兩弧交于點P;連接AP并延長交BC于點E,連接EF.若四邊形ABEF的周長為16,∠C=60°,AG=2![]() ,則四邊形ABEF的面積是( )
,則四邊形ABEF的面積是( )
A.8![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】四邊形ABCD中,對角線AC、BD相交于點O,下列條件不能判定這個四邊形是平行四邊形的是

A.AB∥DC,AD∥BC B.AB=DC,AD=BC
C.AO=CO,BO=DO D.AB∥DC,AD=BC
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:如圖,在矩形ABCD中,M、N分別是邊AD、BC的中點,E、F分別是線段BM、CM的中點

(1)求證:△ABM≌△DCM
(2)判斷四邊形MENF是什么特殊四邊形,并證明你的結論;
(3)當AD:AB= _時,四邊形MENF是正方形(只寫結論,不需證明)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】使得函數值為0的自變量的值稱為函數的零點.例如,對于函數y=x﹣1,令y=0可得x=1,我們說1是函數y=x﹣1的零點.已知函數y=x2﹣2mx﹣2(m+3)(m為常數)
(1)當m=0時,求該函數的零點.
(2)證明:無論m取何值,該函數總有兩個零點.
查看答案和解析>>
科目:初中數學 來源: 題型:
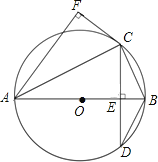
【題目】如圖,AB為⊙O的直徑,弦CD⊥AB,垂足為點E,CF⊥AF,且CF=CE.
(1)求證:CF是⊙O的切線;
(2)若sin∠BAC=![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com