
分析 (1)根據方程的系數結合根的判別式即可得出△=13>0,由此即可得出方程有兩個不相等的實數根;
(2)根據方程的系數結合根的判別式即可得出△=$\frac{41}{4}$>0,由此即可得出方程有兩個不相等的實數根;
(3)根據方程的系數結合根的判別式即可得出△=0,由此即可得出方程有兩個相等的實數根;
(4)根據方程的系數結合根的判別式即可得出△=-$\frac{31}{36}$<0,由此即可得出方程沒有實數根.
解答 解:(1)在方程-x2-3x+1=0中,△=(-3)2-4×(-1)×1=13>0,
∴方程-x2-3x+1=0有兩個不相等的實數根;
(2)在方程2x2-$\frac{7}{2}x$+$\frac{1}{4}$=0中,△=$(-\frac{7}{2})^{2}$-4×2×$\frac{1}{4}$=$\frac{41}{4}$>0,
∴方程2x2-$\frac{7}{2}x$+$\frac{1}{4}$=0有兩個不相等的實數根;
(3)方程可變形為4x2-4$\sqrt{5}$x+5=0,
在方程4x2+5=4$\sqrt{5}$x中,△=$(-4\sqrt{5})^{2}$-4×4×5=0,
∴方程4x2+5=4$\sqrt{5}$x有兩個相等的實數根;
(4)在方程$\frac{2}{3}$x2-$\frac{3}{2}x$+$\frac{7}{6}$=0中,△=$(-\frac{3}{2})^{2}$-4×$\frac{2}{3}$×$\frac{7}{6}$=-$\frac{31}{36}$<0,
∴方程$\frac{2}{3}$x2-$\frac{3}{2}x$+$\frac{7}{6}$=0沒有實數根.
點評 本題考查了根的判別式,熟練掌握“當△>0時,方程有兩個不相等的兩個實數根;當△=0時,方程有兩個相等的兩個實數根;當△<0時,方程無實數根”是解題的關鍵.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:選擇題
| A. | 22017-1 | B. | 22017+1 | C. | 22016-1 | D. | 22016+1 |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
 如圖,在正方形ABCD中,AB=4,E是BC邊的中點,F是CD邊上的一點,且DF=1,若M、N分別是線段AD、AE上的動點,則MN+MF的最小值為$\frac{9\sqrt{5}}{5}$.
如圖,在正方形ABCD中,AB=4,E是BC邊的中點,F是CD邊上的一點,且DF=1,若M、N分別是線段AD、AE上的動點,則MN+MF的最小值為$\frac{9\sqrt{5}}{5}$.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 0個 | B. | 1個 | C. | 2個 | D. | 3個 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
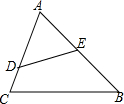 如圖,△ABC中,E為AB中點,AB=6,AC=4.5,∠ADE=∠B,則CD=( )
如圖,△ABC中,E為AB中點,AB=6,AC=4.5,∠ADE=∠B,則CD=( )| A. | $\frac{3}{2}$ | B. | 1 | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com