
【題目】月球是地球的近鄰,它的起源一直是人類不斷探索的謎題之一.全球迄今進行了126次月球探測活動,因為研究月球可提高人類對宇宙的認識,包括認識太陽系的演化及特點,認識地球自然系統與太空自然現象之間的關系.我們已經認識到,在月球表面,白天陽光垂直照射的地方溫度高達127℃,夜晚溫度可降到﹣183℃.下面對“﹣183℃”的敘述不正確的是( )

A. ﹣183是一個負數
B. ﹣183表示在海平面以下183米
C. ﹣183在數軸上的位置在原點的左邊
D. ﹣183是一個比﹣100小的數
科目:初中數學 來源: 題型:
【題目】中國古代數學家們對于勾股定理的發現和證明,在世界數學史上具有獨特的貢獻和地位,體現了數學研究中的繼承和發展.現用4個全等的直角三角形拼成如圖所示“弦圖”.Rt△ABC中,∠ACB=90°,若![]() ,請你利用這個圖形解決下列問題:
,請你利用這個圖形解決下列問題:
(1)試說明![]() ;
;
(2)如果大正方形的面積是10,小正方形的面積是2,求![]() 的值.
的值.

查看答案和解析>>
科目:初中數學 來源: 題型:
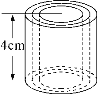
【題目】如圖,圓柱的高是4cm,當圓柱底面半徑r(cm)變化時,圓柱的體積V(cm3)也隨之變化.
(1)在這個變化過程中,寫出自變量,因變量;
(2) 寫出圓柱的體積V與底面半徑r的關系式;
(3)當圓柱的底面半徑由2cm變化到8cm時,圓柱的體積由多少cm3變化到多少cm3.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AB邊的垂直平分線l1交BC于點D,AC邊的垂直平分線l2交BC于點E,l1與l2相交于點O,連接OA,OB,OC.
(1)若△ADE的周長為6 cm,△OBC的周長為16 cm.
①求線段BC的長;
②求線段OA的長.
(2)若∠BAC=120°,求∠DAE的度數.

查看答案和解析>>
科目:初中數學 來源: 題型:
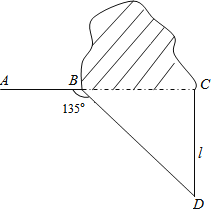
【題目】如圖,修公路遇到一座山,于是要修一條隧道.為了加快施工進度,想在小山的另一側同時施工.為了使山的另一側的開挖點C在AB的延長線上,設想過C點作直線AB的垂線L,過點B作一直線(在山的旁邊經過),與L相交于D點,經測量∠ABD=135°,BD=800米,求直線L上距離D點多遠的C處開挖?(![]() ≈1.414,精確到1米)
≈1.414,精確到1米)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在數軸上,一只螞蟻從原點出發,先向右爬行了4個單位長度到達點A,再向右爬行了2個單位長度到達點B,然后又向左爬行了10個單位長度到達點C.
(1)畫出數軸,并在數軸上表示出A、B、C三點;
(2)根據點C在數軸上的位置,點C可以看作是螞蟻從原點出發,向哪個方向爬行了幾個單位長度得到的?
查看答案和解析>>
科目:初中數學 來源: 題型:
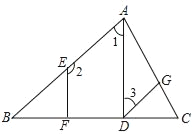
【題目】如圖,已知AD⊥BC,EF⊥BC,垂足分別為D、F,∠2+∠3=180°,試說明:∠GDC=∠B.請補充說明過程,并在括號內填上相應的理由.
解:∵AD⊥BC,EF⊥BC(已知)
∴∠ADB=∠EFB=90° ,
∴EF∥AD( ),
∴ +∠2=180°( ).
又∵∠2+∠3=180°(已知),
∴∠1=∠3( ),
∴AB∥ ( ),
∴∠GDC=∠B( ).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某花圃用花盆培育某種花苗,經過試驗發現每盆的盈利與每盆的株數構成一定的關系,每盆植入3株時,平均單株盈利3元,以同樣的栽培條件,若每盆增加1株,平均單株盈利就減少0.5元,要使每盆的盈利達到10元,每盆應該植多少株? 小明的解法如下:
解:設每盆花苗增加x株,則每盆花苗有(x+3)株,平均單株盈利為(3﹣0.5x)元,
由題意得(x+3)(3﹣0.5x)=10,
化簡,整理得:x2﹣3x+2=0
解這個方程,得:x1=1,x2=2,
答:要使每盆的盈利達到10元,每盆應該植入4株或5株.
(1)本題涉及的主要數量有每盆花苗株數,平均單株盈利,每盆花苗的盈利等,請寫出兩個不同的等量關系: .
(2)請用一種與小明不相同的方法求解上述問題.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】設A是由2×4個整數組成的2行4列的數表,如果某一行(或某一列)各數之和為負數,那么改變該行(或該列)中所有數的符號,稱為一次“操作”.
(1)如表1所示,如果經過兩次“操作”,使得到的數表每行的各數之和與每列的各數之和均為非負整數,請寫出每次“操作”后所得的數表;(寫出一種方法即可)
1 | 2 | 3 | -7 |
-2 | -1 | 0 | 1 |
表1
(2)如表2所示,若經過任意一次“操作”以后,便可使得到的數表每行的各數之和與每列的各數之和均為非負整數,求整數a的值.
a | a2-1 | -a | -a2 |
2-a | 1-a2 | a-2 | a2 |
表2
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com