
【題目】如圖1,拋物線y=﹣ ![]() [(x﹣2)2+n]與x軸交于點A(m﹣2,0)和B(2m+3,0)(點A在點B的左側),與y軸交于點C,連結BC.
[(x﹣2)2+n]與x軸交于點A(m﹣2,0)和B(2m+3,0)(點A在點B的左側),與y軸交于點C,連結BC.
(1)求m、n的值;
(2)如圖2,點N為拋物線上的一動點,且位于直線BC上方,連接CN、BN.求△NBC面積的最大值;
(3)如圖3,點M、P分別為線段BC和線段OB上的動點,連接PM、PC,是否存在這樣的點P,使△PCM為等腰三角形,△PMB為直角三角形同時成立?若存在,求出點P的坐標;若不存在,請說明理由.
【答案】
(1)
解:∵拋物線的解析式為y=﹣ ![]() [(x﹣2)2+n]=﹣
[(x﹣2)2+n]=﹣ ![]() (x﹣2)2﹣
(x﹣2)2﹣ ![]() n,
n,
∴拋物線的對稱軸為直線x=2,
∵點A和點B為對稱點,
∴2﹣(m﹣2)=2m+3﹣2,解得m=1,
∴A(﹣1,0),B(5,0),
把A(﹣1,0)代入y=﹣ ![]() [(x﹣2)2+n]得9+n=0,解得n=﹣9
[(x﹣2)2+n]得9+n=0,解得n=﹣9
(2)
解:作ND∥y軸交BC于D,如圖2,

拋物線解析式為y=﹣ ![]() [(x﹣2)2﹣9]=﹣
[(x﹣2)2﹣9]=﹣ ![]() x2+
x2+ ![]() x+3,
x+3,
當x=0時,y=3,則C(0,3),
設直線BC的解析式為y=kx+b,
把B(5,0),C(0,3)代入得 ![]() ,解得
,解得  ,
,
∴直線BC的解析式為y=﹣ ![]() x+3,
x+3,
設N(x,﹣ ![]() x2+
x2+ ![]() x+3),則D(x,﹣
x+3),則D(x,﹣ ![]() x+3),
x+3),
∴ND=﹣ ![]() x2+
x2+ ![]() x+3﹣(﹣
x+3﹣(﹣ ![]() x+3)=﹣
x+3)=﹣ ![]() x2+3x,
x2+3x,
∴S△NBC=S△NDC+S△NDB= ![]() 5ND=﹣
5ND=﹣ ![]() x2+
x2+ ![]() x=﹣(x﹣
x=﹣(x﹣ ![]() )2+
)2+ ![]() ,
,
當x= ![]() 時,△NBC面積最大,最大值為
時,△NBC面積最大,最大值為 ![]()
(3)
解:存在.
∵B(5,0),C(0,3),
∴BC= ![]() =
= ![]() ,
,
當∠PMB=90°,則∠PMC=90°,△PMC為等腰直角三角形,MP=MC,
設PM=t,則CM=t,MB= ![]() ﹣t,
﹣t,
∵∠MBP=∠OBC,
∴△BMP∽△BOC,
∴ ![]() =
= ![]() =
= ![]() ,即
,即 ![]() =
= ![]() =
= ![]() ,解得t=
,解得t= ![]() ,BP=
,BP= ![]() ,
,
∴OP=OB﹣BP=5﹣ ![]() =
= ![]() ,
,
此時P點坐標為( ![]() ,0);
,0);
當∠MPB=90°,則MP=MC,
設PM=t,則CM=t,MB= ![]() ﹣t,
﹣t,
∵∠MBP=∠CBO,
∴△BMP∽△BCO,
∴ ![]() =
= ![]() =
= ![]() ,即
,即 ![]() =
= ![]() =
= ![]() ,解得t=
,解得t= ![]() ,BP=
,BP= ![]() ,
,
∴OP=OB﹣BP=5﹣ ![]() =
= ![]() ,
,
此時P點坐標為( ![]() ,0);
,0);
綜上所述,P點坐標為( ![]() ,0)或(
,0)或( ![]() ,0).
,0).

【解析】(1)利用拋物線的解析式確定對稱軸為直線x=2,再利用對稱性得到2﹣(m﹣2)=2m+3﹣2,解方程可得m的值,從而得到A(﹣1,0),B(5,0),然后把A點坐標代入y=﹣ ![]() [(x﹣2)2+n]可求出n的值;(2)作ND∥y軸交BC于D,如圖2,利用拋物線解析式確定C(0,3),再利用待定系數法求出直線BC的解析式為y=﹣
[(x﹣2)2+n]可求出n的值;(2)作ND∥y軸交BC于D,如圖2,利用拋物線解析式確定C(0,3),再利用待定系數法求出直線BC的解析式為y=﹣ ![]() x+3,設N(x,﹣
x+3,設N(x,﹣ ![]() x2+
x2+ ![]() x+3),則D(x,﹣
x+3),則D(x,﹣ ![]() x+3),根據三角形面積公式,利用S△NBC=S△NDC+S△NDB可得S△BCN=﹣
x+3),根據三角形面積公式,利用S△NBC=S△NDC+S△NDB可得S△BCN=﹣ ![]() x2+
x2+ ![]() x,然后利用二次函數的性質求解;(3)先利用勾股定理計算出BC=
x,然后利用二次函數的性質求解;(3)先利用勾股定理計算出BC= ![]() ,再分類討論:當∠PMB=90°,則∠PMC=90°,△PMC為等腰直角三角形,MP=MC,設PM=t,則CM=t,MB=
,再分類討論:當∠PMB=90°,則∠PMC=90°,△PMC為等腰直角三角形,MP=MC,設PM=t,則CM=t,MB= ![]() ﹣t,證明△BMP∽△BOC,利用相似比可求出BP的長,再計算OP后可得到P點坐標;當∠MPB=90°,則MP=MC,設PM=t,則CM=t,MB=
﹣t,證明△BMP∽△BOC,利用相似比可求出BP的長,再計算OP后可得到P點坐標;當∠MPB=90°,則MP=MC,設PM=t,則CM=t,MB= ![]() ﹣t,證明△BMP∽△BCO,利用相似比可求出BP的長,再計算OP后可得到P點坐標.本題考查了二次函數的綜合題:熟練掌握二次函數圖象上點的坐標特征和二次函數的性質;會運用待定系數法求函數解析式;理解坐標與圖形的性質;掌握相似三角形的判定,能運用相似比計算線段的長或表示線段之間的關系;學會運用分類討論的思想解決數學問題.
﹣t,證明△BMP∽△BCO,利用相似比可求出BP的長,再計算OP后可得到P點坐標.本題考查了二次函數的綜合題:熟練掌握二次函數圖象上點的坐標特征和二次函數的性質;會運用待定系數法求函數解析式;理解坐標與圖形的性質;掌握相似三角形的判定,能運用相似比計算線段的長或表示線段之間的關系;學會運用分類討論的思想解決數學問題.
【考點精析】本題主要考查了二次函數的性質和比例線段的相關知識點,需要掌握增減性:當a>0時,對稱軸左邊,y隨x增大而減小;對稱軸右邊,y隨x增大而增大;當a<0時,對稱軸左邊,y隨x增大而增大;對稱軸右邊,y隨x增大而減小;如果選用同一長度單位量得兩條線段a,b的長度分別為m,n,那么就說這兩條線段的比是a/b=m/n,或寫成a:b=m:n才能正確解答此題.


 100分闖關期末沖刺系列答案
100分闖關期末沖刺系列答案 名校聯盟快樂課堂系列答案
名校聯盟快樂課堂系列答案科目:初中數學 來源: 題型:
【題目】以下是某省2010年教育發展情況有關數據:
全省共有各級各類學校25000所,其中小學12500所,初中2000所,高中450所,其它學校10050所;全省共有在校學生995萬人,其中小學440萬人,初中200萬人,高中75萬人,其它280萬人;全省共有在職教師48萬人,其中小學20萬人,初中12萬人,高中5萬人,其它11萬人.
請將上述資料中的數據按下列步驟進行統計分析.
(1)整理數據:請設計一個統計表,將以上數據填入表格中.
(2)描述數據:下圖是描述全省各級各類學校所數的扇形統計圖,請將它補充完整.
(3)分析數據:
①分析統計表中的相關數據,小學、初中、高中三個學段的師生比,最小的是哪個學段?請直接寫出.(師生比=在職教師數︰在校學生數)
②根據統計表中的相關數據,你還能從其它角度分析得出什么結論嗎?(寫出一個即可)
③從扇形統計圖中,你得出什么結論?(寫出一個即可)

查看答案和解析>>
科目:初中數學 來源: 題型:
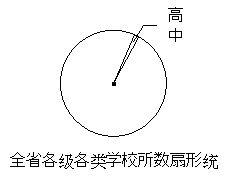
【題目】如圖1,2,3分別以△ABC的AB和AC為邊向△ABC外作正三角形(等邊三角形)、正四邊形(正方形)、正五邊形,BE和CD相交于點O.
(1)在圖1中,求證:△ABE≌△ADC.
(2)由(1)證得△ABE≌△ADC,由此可推得在圖1中∠BOC=120°,請你探索在圖2中,∠BOC的度數,并說明理由或寫出證明過程.
(3)填空:在上述(1)(2)的基礎上可得在圖3中∠BOC=(填寫度數).
(4)由此推廣到一般情形(如圖4),分別以△ABC的AB和AC為邊向△ABC外作正n邊形,BE和CD仍相交于點O,猜想得∠BOC的度數為(用含n的式子表示).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,已知△ABC和△BDE都是等邊三角形.則下列結論:①AE=CD;②BF=BG;③∠AHC=60°;④△BFG是等邊三角形;⑤HB平分∠AHD.其中正確的有( )

A. 2個 B. 3個 C. 4個 D. 5個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(題文)(問題引領)
問題1:在四邊形ABCD中,CB=CD,∠B=∠ADC=90°,∠BCD=120°.E,F分別是AB,AD上的點.且∠ECF=60°.探究圖中線段BE,EF,FD之間的數量關系.
小王同學探究此問題的方法是,延長FD到點G.使DG=BE.連結CG,先證明
△CBE≌△CDG,再證明△CEF≌△CGF.他得出的正確結論是________________.

(探究思考)
問題2:若將問題1的條件改為:四邊形ABCD中,CB=CD,∠ABC+∠ADC=180°,
∠ECF= ![]() ∠BCD, 問題1的結論是否仍然成立?請說明理由.
∠BCD, 問題1的結論是否仍然成立?請說明理由.

(拓展延伸)
問題3:在問題2的條件下,若點E在AB的延長線上,點F在DA的延長線上,則問題2的結論是否仍然成立?若不成立,猜測此時線段BE、DF、EF之間存在什么樣的等量關系?并說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,正方形網格中的每個小正方形邊長都是1,每個小格的頂點叫做格點,以格點為頂點分別按下列要求畫三角形.
(1)在圖1中,畫一個三角形,使它的三邊長都是有理數; 
(2)在圖2中,畫一個直角三角形,使它們的三邊長都是無理數; 
(3)在圖3中,畫一個正方形,使它的面積是10. 
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,河邊有A,B兩個村莊,A村距河邊10 m,B村距河邊30 m,兩村平行于河邊方向的水平距離為30 m,現要在河邊建一抽水站,需鋪設管道抽水到A村和B村.
(1)求鋪設管道的最短長度是多少,請畫圖說明;
(2)若鋪設管道每米需要500元,則最低費用為多少?

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com