
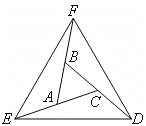
【題目】已知,如圖,延長![]() 的各邊,使得
的各邊,使得![]() ,
,![]() ,順次連接
,順次連接![]() ,得到
,得到![]() 為等邊三角形.
為等邊三角形.
求證:(1)![]() ;(2)
;(2)![]() 為等邊三角形.
為等邊三角形.
【答案】(1)證明見解析;(2)證明見解析
【解析】(1)關鍵是證出CE=AF,可由AE=AB,AC=BF,兩兩相加可得.再結合已知條件可證出△AEF≌△CDE.
(2)有(1)中的全等關系,可得出∠AFE=∠CED,再結合△DEF是等邊三角形,可知∠DEF=60°,從而得出∠BAC=60°,同理可得∠ACB=60°,那么∠ABC=60°.因而△ABC是等邊三角形.
證明:(1)∵BF=AC,AB=AE(已知)
∴FA=EC(等量加等量和相等).
∵△DEF是等邊三角形(已知),
∴EF=DE(等邊三角形的性質).
又∵AE=CD(已知),
∴△AEF≌△CDE(SSS).
(2)由△AEF≌△CDE,得∠FEA=∠EDC(對應角相等),
∵∠BCA=∠EDC+∠DEC=∠FEA+∠DEC=∠DEF(等量代換)
△DEF是等邊三角形(已知),
∴∠DEF=60°(等邊三角形的性質),
∴∠BCA=60°(等量代換),
由△AEF≌△CDE,得∠EFA=∠DEC,
∵∠DEC+∠FEC=60°,
∴∠EFA+∠FEC=60°,
又∠BAC是△AEF的外角,
∴∠BAC=∠EFA+∠FEC=60°,
∴△ABC中,AB=BC(等角對等邊).
∴△ABC是等邊三角形(等邊三角形的判定).


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】在電影院內,如果將“12排8號”記作(12,8),那么“5排9號”怎樣表示?(23,15)表示的含義是什么?( )
A. (9,5);23排15號 B. (5,9);23排15號
C. (9,5);15排23號 D. (5,9);15排23號
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】把下列各數分別填入相應的集合里.
-5, ![]() ,0,-3.14,
,0,-3.14, ![]() ,
, ![]() ,2014,+1.99,-(-6),-2.101001000….
,2014,+1.99,-(-6),-2.101001000….
(1)正數集合:{________________________…};
(2)負數集合:{_______________________________…};
(3)非負整數集合:{________________________…};
(4)負分數集合:{_______________________…}.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】有以下兩個結論:
① 任何一個有理數和它的相反數之間至少有一個有理數;
② 如果一個有理數有倒數,則這個有理數與它的倒數之間至少有一個有理數。
則( )
A. ①,②都不對; B. ①對,②不對; C. ①,②都對; D. ①不對,②對;
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列多項式乘法,能用平方差公式進行計算的是( )
A.(x+y)(-x-y)
B.(2x+3y)(2x-3z)
C.(-a-b)(a-b)
D.(m-n)(n-m)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列多項式乘法,不能用平方差公式計算的是( )
A.(-a-b)(-b+a)
B.(xy+z)(xy-z)
C.(-2a-b)(2a+b)
D.(0.5x-y)(-y-0.5x)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com