
(滿分l6分)如圖5—9,已知點(diǎn)O為坐標(biāo)原點(diǎn),∠AOB=30°,∠ABO=90°,且點(diǎn)A的坐標(biāo)為(2,0)。
(1)求點(diǎn)B的坐標(biāo);
(2)若二次函數(shù)y=ax2+bx+c的圖象經(jīng)過A,B,O三點(diǎn),求此二次函數(shù)的解析式;
(3)在(2)中的二次函數(shù)圖象的OB段(不包括點(diǎn)O,B)上,是否存在一點(diǎn)C,使得四邊形ABCO的面積最大?若存在,求出這個最大值及此時點(diǎn)C的坐標(biāo);若不存在,請說明理由。
解:(1)在Rt△OAB中,∵∠AOB=30°,∴OB=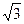 .過點(diǎn)B作x
.過點(diǎn)B作x
軸的垂線BD,垂足為D,如圖D5—4所示.則OD= ,BD=
,BD=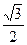 ,∴點(diǎn)
,∴點(diǎn)
B的坐標(biāo)為( ,
,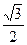 ). ……2分
). ……2分
(2)將A(2,0),B( ,
,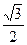 ),O(0,0)三點(diǎn)的坐標(biāo)代入y=ax2+bx+c,得
),O(0,0)三點(diǎn)的坐標(biāo)代入y=ax2+bx+c,得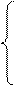 4a+2b+c
4a+2b+c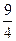 a+
a+ b+c=
b+c=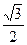 , ……4分
, ……4分
c=0.
解方程組,得a=一 ,b=
,b=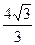 .c="0 " ……5分
.c="0 " ……5分
∴所求二次函數(shù)解析式是y=一 x2 +
x2 +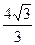 x. ……6分
x. ……6分
(3)設(shè)存在點(diǎn)c(x,一 x2 +
x2 +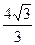 x)(其中0<x<
x)(其中0<x< ),使四邊形ABCO面積最大.
),使四邊形ABCO面積最大.
∵△OAB面積為定值,即S△OAB=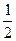 OA·BD=
OA·BD=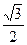 .
.
∴只要△OBC面積最大,四邊形ABCO面積就最大. ……8分
如圖D5—4,過點(diǎn)C作x軸的垂線CE,垂足為點(diǎn)E,交OB于點(diǎn)F,則
S△OBC=S△OCF+S△BCF=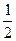 ︱CF︱·︱OE︱+
︱CF︱·︱OE︱+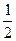 ︱CF︱·︱ED︱=
︱CF︱·︱ED︱=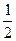 ︱CF︱·︱OD︱=
︱CF︱·︱OD︱=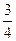 ︱CF︱. ……9分
︱CF︱. ……9分
而︱CF︱=yC-yF=- x2+
x2+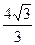 x-
x-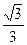 x=-
x=- x2+
x2+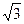 x,
x,
∴S△OBC=-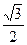 x2+
x2+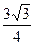 x=-
x=-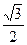 (x-
(x-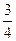 )2+
)2+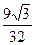 . ……12分
. ……12分
∴當(dāng)x=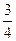 時,△OBC最大面積, 最大面積為
時,△OBC最大面積, 最大面積為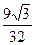 . ……l4分
. ……l4分
此時,點(diǎn)C坐標(biāo)為(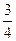 ,
,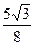 ),四邊形ABCO的面積為
),四邊形ABCO的面積為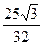 . ……16分
. ……16分
解析


 期末1卷素質(zhì)教育評估卷系列答案
期末1卷素質(zhì)教育評估卷系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com