
【題目】如圖,已知點E,F分別是ABCD的邊BC,AD上的中點,且∠BAC=90°. 
(1)求證:四邊形AECF是菱形;
(2)若∠B=30°,BC=10,求菱形AECF面積.
【答案】
(1)證明:∵四邊形ABCD是平行四邊形,
∴AD=BC,
在Rt△ABC中,∠BAC=90°,點E是BC邊的中點,
∴AE= ![]() BC=CE,
BC=CE,
同理,AF= ![]() AD=CF,
AD=CF,
∴AE=CE=AF=CF,
∴四邊形AECF是菱形
(2)解:連接EF交AC于點O,如圖所示:
在Rt△ABC中,∠BAC=90°,∠B=30°,BC=10,
∴AC= ![]() BC=5,AB=
BC=5,AB= ![]() AC=5
AC=5 ![]() ,
,
∵四邊形AECF是菱形,
∴AC⊥EF,OA=OC,
∴OE是△ABC的中位線,
∴OE= ![]() AB=
AB= ![]() ,
,
∴EF=5 ![]() ,
,
∴菱形AECF的面積= ![]() ACEF=
ACEF= ![]() ×5×5
×5×5 ![]() =
= ![]() .
.

【解析】(1)由平行四邊形的性質得出AD=BC,由直角三角形斜邊上的中線性質得出AE= ![]() BC=CE,AF=
BC=CE,AF= ![]() AD=CF,得出AE=CE=AF=CF,即可得出結論;(2)連接EF交AC于點O,解直角三角形求出AC、AB,由三角形中位線定理求出OE,得出EF,菱形AECF的面積=
AD=CF,得出AE=CE=AF=CF,即可得出結論;(2)連接EF交AC于點O,解直角三角形求出AC、AB,由三角形中位線定理求出OE,得出EF,菱形AECF的面積= ![]() ACEF,即可得出結果.
ACEF,即可得出結果.


 一線名師權威作業本系列答案
一線名師權威作業本系列答案科目:初中數學 來源: 題型:
【題目】一輛出租車從A地出發,在一條東西走向的街道上往返,每次行駛的情況(記向東為正)記錄如下(x>5且x<14,單位:m):
行駛次數 | 第一次 | 第二次 | 第三次 | 第四次 |
行駛情況 | x | ﹣ | x﹣3 | 2(5﹣x) |
行駛方向(填“東”或“西”) |
|
|
|
|
(1)請將表格補充完整;
(2)求經過連續4次行駛后,這輛出租車所在的位置;
(3)若出租車行駛的總路程為41m,求第一次行駛的路程x的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】先閱讀下列解題過程,然后回答問題:
解方程: ![]()
解:①當![]() ≥0時,原方程可化為:
≥0時,原方程可化為: ![]() ,解得
,解得![]() ;
;
②當![]() <0時,原方程可化為:
<0時,原方程可化為: ![]() ,解得
,解得![]() ;
;
所以原方程的解是![]() 或
或![]()
(1)解方程: ![]()
(2)探究:當![]() 為何值時,方程
為何值時,方程![]() ①無解;②只有一個解;③有兩個解。
①無解;②只有一個解;③有兩個解。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知,如圖,∠MON=45°,OA1=1,作正方形A1B1C1A2 , 周長記作C1;再作第二個正方形A2B2C2A3 , 周長記作C2;繼續作第三個正方形A3B3C3A4 , 周長記作C3;點A1、A2、A3、A4…在射線ON上,點B1、B2、B3、B4…在射線OM上,…依此類推,則第n個正方形的周長Cn= . 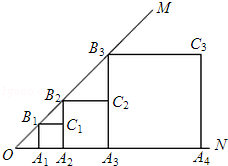
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列變形中:
①由方程![]() =2去分母,得x﹣12=10;
=2去分母,得x﹣12=10;
②由方程![]() x=
x=![]() 兩邊同除以
兩邊同除以![]() ,得x=1;
,得x=1;
③由方程6x﹣4=x+4移項,得7x=0;
④由方程2﹣![]() 兩邊同乘以6,得12﹣x﹣5=3(x+3).
兩邊同乘以6,得12﹣x﹣5=3(x+3).
錯誤變形的個數是( )個.
A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
科目:初中數學 來源: 題型:
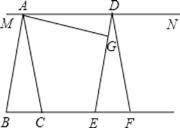
【題目】如圖所示,將![]() 沿直線BC方向平移
沿直線BC方向平移![]() 的位置,G是DE上一點,連接AG,過點A、D作直線MN.
的位置,G是DE上一點,連接AG,過點A、D作直線MN.
(1)求證:![]() ;
;
(2)若![]() ,
,![]() ,判斷AG與DE的位置關系,并證明你的結論.
,判斷AG與DE的位置關系,并證明你的結論.
查看答案和解析>>
科目:初中數學 來源: 題型:
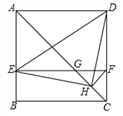
【題目】如圖,在正方形ABCD中,AC為對角線,E為AB上一點,過點E作![]() ,與AC、DC分別交于點
,與AC、DC分別交于點![]() 為CG的中點,連結DE、EH、DH、
為CG的中點,連結DE、EH、DH、![]() 下列結論:
下列結論: ![]() ;
; ![]() ≌
≌![]() ;
; ![]() ;
; ![]() 若
若![]() ,則
,則![]() 其中結論正確的有
其中結論正確的有![]()
A. 1個 B. 2個 C. 3個 D. 4個
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com