
【題目】已知如圖:拋物線![]() 與
與![]() 軸交于
軸交于![]() 兩點(點
兩點(點![]() 在點
在點![]() 的左側)與
的左側)與![]() 軸交于點
軸交于點![]() ,點
,點![]() 為拋物線的頂點,過點
為拋物線的頂點,過點![]() 的對稱軸交
的對稱軸交![]() 軸于點
軸于點![]() .
.
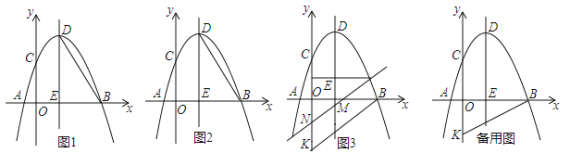
(1)如圖1,連接![]() ,試求出直線
,試求出直線![]() 的解析式;
的解析式;
(2)如圖2,點![]() 為拋物線第一象限上一動點,連接
為拋物線第一象限上一動點,連接![]() ,
,![]() ,
,![]() ,當四邊形
,當四邊形![]() 的面積最大時,線段
的面積最大時,線段![]() 交
交![]() 于點
于點![]() ,求此時
,求此時![]() :
:![]() 的值;
的值;
(3)如圖3,已知點![]() ,連接
,連接![]() ,將
,將![]() 沿著
沿著![]() 軸上下平移(包括
軸上下平移(包括![]() )在平移的過程中直線
)在平移的過程中直線![]() 交
交![]() 軸于點
軸于點![]() ,交
,交![]() 軸于點
軸于點![]() ,則在拋物線的對稱軸上是否存在點
,則在拋物線的對稱軸上是否存在點![]() ,使得
,使得![]() 是以
是以![]() 為直角邊的等腰直角三角形,若存在,請直接寫出點
為直角邊的等腰直角三角形,若存在,請直接寫出點![]() 的坐標,若不存在,請說明理由.
的坐標,若不存在,請說明理由.
【答案】(1)y=-![]() x+
x+![]() ;(2)
;(2)![]() ;(3)G1(2,
;(3)G1(2,![]() ),G2(2,-7),G3(2,-3)G4(2,-
),G2(2,-7),G3(2,-3)G4(2,-![]() )
)
【解析】
試題分析:(1)根據自變量與函數值的對應關系,可得A、B點坐標,根據頂點坐標的定義,可得D點坐標,根據待定系數法,可得答案;
(2)根據平行于BC且與拋物線相切,可得過P點平行BC的直線,根據解方程組,可得P點坐標,根據解方程組,可得F點坐標,根據相似三角形的性質,可得答案;
(3)根據平移的性質,可得直線MN的解析式,根據全等三角形的判定與性質,可得關于b的方程,根據解方程,可得b,根據b的值,可得OM的長,可得EG的長,可得答案.
試題解析:(1)在y=-![]() x2+2x+
x2+2x+![]() 中,
中,
令y=0,則-![]() x2+2x+
x2+2x+![]() =0,
=0,
解得:x1=-1.x2=5,
則A的坐標是(-1,0),B的坐標是(5,0).
拋物線y=-![]() x2+2x+
x2+2x+![]() 的對稱軸是x=2,
的對稱軸是x=2,
把x=2代入解析式得y=![]() ,則D的坐標是(2,
,則D的坐標是(2,![]() ).
).
設直線BD的解析式是y=kx+b,
根據題意得: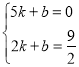 ,
,
解得: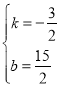 ,
,
則直線BD的解析式是y=-![]() x+
x+![]() ;
;
(2)連接BC,如圖2,
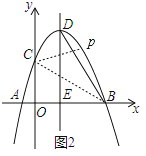
y=-![]() x2+2x+
x2+2x+![]() 中,令x=0,則y=
中,令x=0,則y=![]() ,則C的坐標是(0,
,則C的坐標是(0,![]() ).
).
設BC的解析式是y=mx+n,
則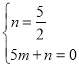 ,
,
解得: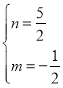 ,
,
則直線BC的解析式是y=-![]() x+
x+![]() .
.
設與BC平行且與拋物線只有一個公共點的直線的解析式是y=-![]() x+d.
x+d.
則-![]() x2+2x+
x2+2x+![]() =-
=-![]() x+d,
x+d,
即x2-5x+(2d-10)=0,
當△=0時,x=![]() ,
,
代入y=-![]() x2+2x+
x2+2x+![]() 中得:y=
中得:y=![]() ,
,
則P的坐標是(![]() ,
, ![]() ).
).
又∵C的坐標是(0,![]() ),
),
設CP的解析式是y=ex+f,則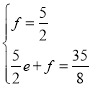
解得: ,
,
則直線CP的解析式是y=![]() x+
x+![]() .
.
根據題意得: ,
,
解得: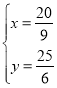 ,
,
則F的坐標是(![]() ,
,![]() ).
).
則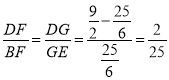 ;
;
(3)如圖3,
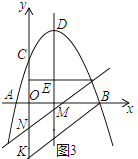
設BK的解析式是y=kx+b,
則![]() ,
,
解得: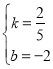 ,
,
則直線BK的解析式是y=![]() x-2,
x-2,
MN的解析式為y=![]() x+b,
x+b,
當y=0時,x=-![]() b,即M(-
b,即M(-![]() b,0),ME=-
b,0),ME=-![]() b-2.
b-2.
當x=0時,y=b,即N(0,b).
由△GMN是以MN為腰的等腰直角三角形,得
MG=MN,∠GMN=90°.
∵∠MGE+∠GME=90°,∠GME+∠EMN=90°,
∴∠MGE=∠AMN.
在△GME和△MNA中,
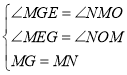 ,
,
∴△GME≌△MNO(AAS),
∴ME=ON,EG=OM,
即-![]() b-2=-b.
b-2=-b.
解得b=-![]() .
.
EG=OM=-![]() b=
b=![]() ,
,
G1點的坐標為(2,![]() ).
).
同理可求:G2(2,-7),G3(2,-3)G4(2,-![]() )
)


科目:初中數學 來源: 題型:
【題目】若拋物線![]() 與
與![]() 滿足
滿足![]() ,則稱
,則稱![]() 互為“相關拋物線”給出如下結論:
互為“相關拋物線”給出如下結論:
①y1與y2的開口方向,開口大小不一定相同; ②y1與y2的對稱軸相同;③若y2的最值為m,則y1的最值為k2m;④若函數![]() 與x 軸的兩交點間距離為d,則函數
與x 軸的兩交點間距離為d,則函數![]() 與x 軸的兩交點間距離也為
與x 軸的兩交點間距離也為![]() .其中正確的結論的序號是___________(把所有正確結論的序號都填在橫線上).
.其中正確的結論的序號是___________(把所有正確結論的序號都填在橫線上).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某電子商投產一種新型電子產品,每件制造成本為18元,試銷過程發現,每月銷量y(萬件)與銷售單價x(元)之間關系可以近似地看作一次函數![]() .
.
(1)寫出每月的利潤z(萬元)與銷售單價x(元)之間函數解析式(利潤=售價-制造成本);
(2)當銷售單價為多少元時,廠商每月能夠獲得350萬元的利潤?當銷售單價為多少元時,廠商每月能夠獲得最大利潤?最大利潤是多少?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com