
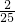 S△BCD?若存在,求出此時t的值;若不存在,說明理由;
S△BCD?若存在,求出此時t的值;若不存在,說明理由;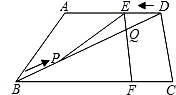
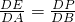 .
.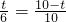 ,
,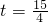 ,
,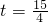 (s),PE∥AB.
(s),PE∥AB.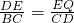 .
.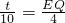 .
.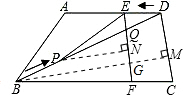
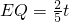 .
. CD=2cm,
CD=2cm,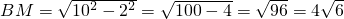 cm,
cm,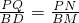 .
.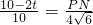 .
.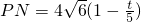 .
. EQ•PN=
EQ•PN= ×
×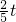 ×
×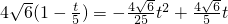 .
. CD•BM=
CD•BM= ×4×4
×4×4 =8
=8 ,
,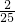 S△BCD,
S△BCD,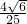 t2+
t2+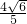 t=
t=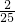 ×8
×8 ,
, .
.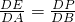 ,故用t表示DE和DP后,代入上式求得t的值;
,故用t表示DE和DP后,代入上式求得t的值;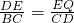 ,求得EQ的值,再由△PNQ∽△BMD,得到
,求得EQ的值,再由△PNQ∽△BMD,得到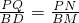 ,求得PN的值,利用S△PEQ=
,求得PN的值,利用S△PEQ= EQ•PN得到y與t之間的函數關系式;
EQ•PN得到y與t之間的函數關系式;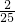 S△BCD建立方程,求得t的值;
S△BCD建立方程,求得t的值;

 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:
 如圖,在梯形ABCD中,AD∥BC,∠BCD=90°,以CD為直徑的半圓O切AB于點E,這個梯形的面積為21cm2,周長為20cm,那么半圓O的半徑為( )
如圖,在梯形ABCD中,AD∥BC,∠BCD=90°,以CD為直徑的半圓O切AB于點E,這個梯形的面積為21cm2,周長為20cm,那么半圓O的半徑為( )| A、3cm | B、7cm | C、3cm或7cm | D、2cm |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com