
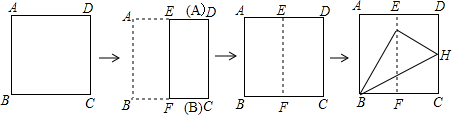
分析 先連接CG,根據折疊的性質,得出△BCG是等邊三角形,進而得出∠CBG=60°,再根據∠CBH=$\frac{1}{2}$∠CBG進行計算即可.
解答 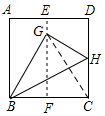 解:連接CG,
解:連接CG,
由折疊可得,BC=AB=BG,
∵EF是正方形ABCD的對稱軸,
∴GB=GC,
∴BC=CG=GB,
∴△BCG是等邊三角形,
∴∠CBG=60°,
由折疊可得,∠CBH=$\frac{1}{2}$∠CBG=30°,
故答案為:30°.
點評 本題是折疊問題,主要考查了正方形的性質,折疊的性質以及等邊三角形的判定與性質,解決問題的關鍵是作輔助線構造等邊三角形,解題時注意:折疊是一種對稱變換,它屬于軸對稱,折疊前后圖形的形狀和大小不變,位置變化,對應邊和對應角相等.


 應用題天天練四川大學出版社系列答案
應用題天天練四川大學出版社系列答案科目:初中數學 來源: 題型:解答題
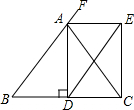 如圖所示,△ABC中,AB=AC,AD是BC邊上的高,AE是∠CAF的平分線且∠CAF是△ABC的一個外角,且DE∥BA,四邊形ADCE是矩形嗎?為什么?
如圖所示,△ABC中,AB=AC,AD是BC邊上的高,AE是∠CAF的平分線且∠CAF是△ABC的一個外角,且DE∥BA,四邊形ADCE是矩形嗎?為什么?查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 65πcm2 | B. | 90πcm2 | C. | 155πcm2 | D. | 209πcm2 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | x2-1+y2=(x-1)(x+1)+y2 | B. | x(a-b)=ax-bx | ||
| C. | ax+bx+c=x(a+b)+c | D. | x2-1=(x+1)(x-1) |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com