Question

已知∠AOB內有一點P，試在OA、OB上求點M、N，使△PMN的周長最短．（要求尺規作圖，寫出作法步驟證明）

Answer 1

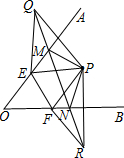
證明：由對稱點的性質可知，
OA為PQ的中垂線，
故PM=QM．
同理：PN=NR．
∴△PMN的周長=線段QR的長，
當在OA，OB上取其它點E，F時，如圖中△PEF，
△PEF的周長=PE+EF+PF=QE+EF+RF，
顯然QE+EF+RF＞QR，
∴△PMN為周長最短的三角形．
分析：先根據軸對稱的性質作出P關于OA、OB的對稱點Q、R，連接QR，與OA、OB交點即為M、N．再在OA、OB上另取E、F，根據兩點之間線段最短得到QR為最短距離．
點評：此題考查了軸對稱---最短路徑問題，將三角形的周長轉化為直線和折線的長度再進行比較是解答此題的關鍵．