
 .
.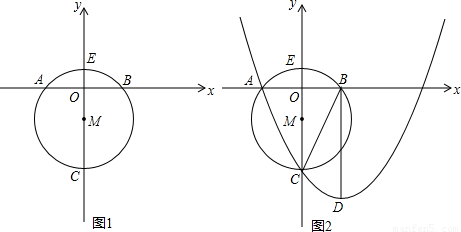
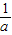 =4并求得a的值即可;
=4并求得a的值即可;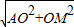 =5,
=5, =-2+
=-2+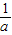 ;
; =±5,
=±5, 或a=-
或a=- 時,拋物線的對稱軸與⊙M相切;
時,拋物線的對稱軸與⊙M相切; =
= ,
, ,
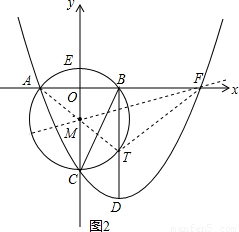
,
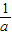 =4,
=4, ;
;

科目:初中數學 來源: 題型:
 23、在數學上,為了確定平面上點的位置,我們常用下面的方法:如圖甲,在平面內畫兩條互相垂直,并且有公共原點O的數軸,通常一條畫成水平,叫x軸,另一條畫成鉛垂,叫y軸,這樣,我們就說在平面上建立了一個平面直角坐標系,這是由法國數學家和哲學家笛卡爾創立的,這樣我們就能確定平面上點的位置,例如,要確定點M的位置,只要作MP⊥x軸,MP⊥y軸,設垂足N,P在各自數軸上所表示的數分別為x,y,則x叫做點M的橫坐標,y叫做點M的縱坐標,有序數對(x,y)叫做M點的坐標,如圖甲,點M的坐標記作(2,3),(1)△ABC在平面直角坐標系中的位置如圖乙,請把△ABC向右平移3個單位,在平面直角坐標系中畫出平移后的△A′B′C′;
23、在數學上,為了確定平面上點的位置,我們常用下面的方法:如圖甲,在平面內畫兩條互相垂直,并且有公共原點O的數軸,通常一條畫成水平,叫x軸,另一條畫成鉛垂,叫y軸,這樣,我們就說在平面上建立了一個平面直角坐標系,這是由法國數學家和哲學家笛卡爾創立的,這樣我們就能確定平面上點的位置,例如,要確定點M的位置,只要作MP⊥x軸,MP⊥y軸,設垂足N,P在各自數軸上所表示的數分別為x,y,則x叫做點M的橫坐標,y叫做點M的縱坐標,有序數對(x,y)叫做M點的坐標,如圖甲,點M的坐標記作(2,3),(1)△ABC在平面直角坐標系中的位置如圖乙,請把△ABC向右平移3個單位,在平面直角坐標系中畫出平移后的△A′B′C′;查看答案和解析>>
科目:初中數學 來源: 題型:
 在平面直角坐標系中,將一塊腰長為2
在平面直角坐標系中,將一塊腰長為2| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
查看答案和解析>>
科目:初中數學 來源:同步輕松練習 八年級 數學 上 題型:059
學校閱覽室有能坐4人的方桌,如果多于4人,就把方桌拼成一行,2張方桌拼成一行能坐6人(如圖)

(1)按照這種規定填寫下表:
(2)根據表中的數據,將s作為縱坐標,n作為橫坐標,在如圖所示的平面直角坐標系中找出相應各點.

(3)請你猜一猜上述各點會在某一個函數圖象上嗎?如果在某一函數圖象上,求出該函數的解析式,并利用你探求的結果,求出當n=10時,s的值.
查看答案和解析>>
科目:初中數學 來源:2013-2014學年北京海淀區九年級第一學期期中測評數學試卷(解析版) 題型:解答題
閱讀下面的材料:
小明在研究中心對稱問題時發現:
如圖1,當點 為旋轉中心時,點
為旋轉中心時,點 繞著點
繞著點 旋轉180°得到
旋轉180°得到 點,點
點,點 再繞著點
再繞著點 旋轉180°得到
旋轉180°得到 點,這時點
點,這時點 與點
與點 重合.
重合.
如圖2,當點 、
、 為旋轉中心時,點
為旋轉中心時,點 繞著點
繞著點 旋轉180°得到
旋轉180°得到 點,點
點,點 繞著點
繞著點 旋轉180°得到
旋轉180°得到 點,點
點,點 繞著點
繞著點 旋轉180°得到
旋轉180°得到 點,點
點,點 繞著點
繞著點 旋轉180°得到
旋轉180°得到 點,小明發現P、
點,小明發現P、 兩點關于點
兩點關于點 中心對稱.
中心對稱.



(1)請在圖2中畫出點 、
、 ,
小明在證明P、
,
小明在證明P、 兩點關于點
兩點關于點 中心對稱時,除了說明P、
中心對稱時,除了說明P、 、
、 三點共線之外,還需證明;
三點共線之外,還需證明;
(2)如圖3,在平面直角坐標系xOy中,當 、
、 、
、 為旋轉中心時,點
為旋轉中心時,點 繞著點
繞著點 旋轉180°得到
旋轉180°得到 點;點
點;點 繞著點
繞著點 旋轉180°得到
旋轉180°得到 點;點
點;點 繞著點
繞著點 旋轉180°得到
旋轉180°得到 點;點
點;點 繞著點
繞著點 旋轉180°得到點
旋轉180°得到點 . 繼續如此操作若干次得到點
. 繼續如此操作若干次得到點 ,則點
,則點 的坐標為(),點
的坐標為(),點 的坐為.
的坐為.
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 ,有序數對(x,y)叫做M點的坐標,如圖甲,點M的坐標記作(2,3),
,有序數對(x,y)叫做M點的坐標,如圖甲,點M的坐標記作(2,3),查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com