
【題目】在平面直角坐標系xOy中,若點P和點![]() 關于x軸對稱,點
關于x軸對稱,點![]() 和點
和點![]() 關于直線l對稱,則稱點
關于直線l對稱,則稱點![]() 是點P關于x軸,直線l的二次對稱點.
是點P關于x軸,直線l的二次對稱點.
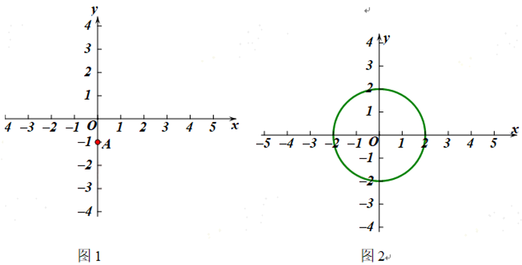
(1)如圖1,點A(0,-1).
①若點B是點A關于x軸,直線![]() :x=2的二次對稱點,則點B的坐標為 ;
:x=2的二次對稱點,則點B的坐標為 ;
②點C (-4,1)是點A關于x軸,直線![]() :x=a的二次對稱點,則a的值為 ;
:x=a的二次對稱點,則a的值為 ;
③點D(-1,0)是點A關于x軸,直線![]() 的二次對稱點,則直線
的二次對稱點,則直線![]() 的表達式為 ;
的表達式為 ;
(2)如圖2,O的半徑為2.若O上存在點M,使得點M′是點M關于x軸,直線![]() :x = b的二次對稱點,且點M′在射線
:x = b的二次對稱點,且點M′在射線![]() (x≥0)上,b的取值范圍是 ;
(x≥0)上,b的取值范圍是 ;
(3)E(0,t)是y軸上的動點,E的半徑為2,若E上存在點N,使得點N′是點N關于x軸,直線![]() :
:![]() 的二次對稱點,且點N′在x軸上,求t的取值范圍.
的二次對稱點,且點N′在x軸上,求t的取值范圍.
【答案】(1)①(4,1),②-2,③y =- x;(2)b的取值范圍是-1≤b≤![]() ;(3)-4≤t≤4
;(3)-4≤t≤4
【解析】
(1)①根據題目中二次對稱點的定義,可以求得點B的坐標;
②根據題目中二次對稱點的定義,可以求得a的值;
③根據題目中二次對稱點的定義,可以求得直線l3的表達式;
(2)根據題意可以畫出相應的圖形,利用分類討論的方法即可解答本題;
(3)根據題意和對稱的二次對稱點的定義,根據題目中的圖形,可以求得t的取值范圍,本題得以解決.
解:(1)① 點B的坐標為 (4,1)
② a的值為-2
③直線l3的表達式為y =- x
(2)如圖2,
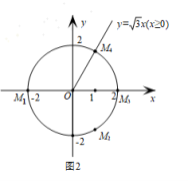
設O與x軸的兩個交點為![]() (-2,0),
(-2,0),![]() (2,0),
(2,0),
與射線![]() (x≥0)的交點為
(x≥0)的交點為![]() ,則
,則![]() 的坐標為(1,
的坐標為(1,![]() ).
).
![]() 關于x軸的對稱點為
關于x軸的對稱點為![]() .
.
當點M在![]() 的位置時,b=-1,
的位置時,b=-1,
當點M在![]() 的位置時,b=1,
的位置時,b=1,
當點M在![]() 的位置時,b=1,
的位置時,b=1,
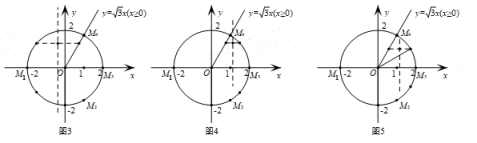
當點M在劣弧![]() 上時(如圖3),-1≤b≤1,
上時(如圖3),-1≤b≤1,
當點M在劣弧![]() 上時(如圖4),b的值比1大,當到劣弧
上時(如圖4),b的值比1大,當到劣弧![]() 的中點時,達到最大值(如圖5),最大值為
的中點時,達到最大值(如圖5),最大值為![]() .綜上,b的取值范圍是-1≤b≤
.綜上,b的取值范圍是-1≤b≤![]() .
.
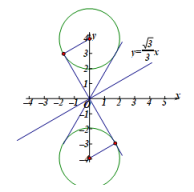
(3)∵x軸和直線![]() 關于直線
關于直線![]() 對稱,
對稱,
直線![]() 和直線
和直線![]() 關于x軸對稱,
關于x軸對稱,
∴E只要與直線![]() 和
和![]() 有交點即可.
有交點即可.
∴t 的取值范圍是:-4≤t≤4
. 


科目:初中數學 來源: 題型:
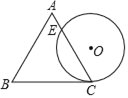
【題目】如圖是某商品標牌的示意圖,⊙O與等邊△ABC的邊BC相切于點C,且⊙O的直徑與△ABC的高相等,已知等邊△ABC邊長為4,設⊙O與AC相交于點E,則AE的長為( )
A.![]() B.1C.
B.1C.![]() ﹣1D.
﹣1D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】對于平面內![]() 和
和![]() 外一點
外一點![]() ,若過點
,若過點![]() 的直線
的直線![]() 與
與![]() 有兩個不同的公共點
有兩個不同的公共點![]() ,點
,點![]() 為直線
為直線![]() 上的另一點,且滿足
上的另一點,且滿足![]() (如圖1所示),則稱點
(如圖1所示),則稱點![]() 是點
是點![]() 關于
關于![]() 的密切點.
的密切點.
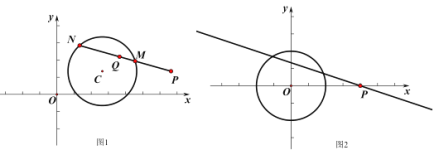
已知在平面直角坐標系![]() 中,
中, ![]() 的半徑為2,點
的半徑為2,點![]() .
.
(1)在點![]()
![]() 中,是點
中,是點![]() 關于
關于![]() 的密切點的為__________.
的密切點的為__________.
(2)設直線![]() 方程為
方程為![]() ,如圖2所示,
,如圖2所示,
①![]() 時,求出點
時,求出點![]() 關于
關于![]() 的密切點
的密切點![]() 的坐標;
的坐標;
②![]() 的圓心為
的圓心為![]() ,半徑為2,若
,半徑為2,若![]() 上存在點
上存在點![]() 關于
關于![]() 的密切點,直接寫出
的密切點,直接寫出![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
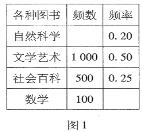
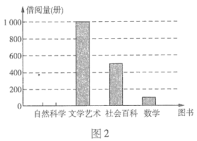
【題目】某中學圖書館將圖書分為自然科學、文學藝術、社會百科、數學四類在“讀書月”活動中,為了了解圖書的借閱情況,圖書管理員對本月各類圖書的借閱進行了統計,圖1和圖2是圖書管理員通過采集數據后繪制的兩幅不完整的頻率分布表與頻數分布條形圖.請你根據圖表中提供的信息,解答以下問題:
(1)填充圖1頻率分布表中的空格;
(2)在圖2中,將表示“自然科學”的部分補充完整;
(3)若該學校打算采購一萬冊圖書,請你估算“數學”類圖書應采購多少冊較合適?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】二次函數![]() 上部分點的橫坐標x與縱坐標y的對應值如下表:
上部分點的橫坐標x與縱坐標y的對應值如下表:
x | … |
|
| 0 | 1 | 2 | 3 | … |
y | … | 3 |
| 0 |
| 0 | m | … |

(1)直接寫出此二次函數的對稱軸 ;
(2)求b的值;
(3)直接寫出表中的m值,m= ;
(4)在平面直角坐標系xOy中,畫出此二次函數的圖象.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】若一個三角形一條邊的平方等于另兩條邊的乘積,我們把這個三角形叫做比例三角形.

![]() 已知
已知![]() 是比例三角形,
是比例三角形,![]() ,
,![]() ,請直接寫出所有滿足條件的AC的長;
,請直接寫出所有滿足條件的AC的長;
![]() 如圖1,在四邊形ABCD中,
如圖1,在四邊形ABCD中,![]() ,對角線BD平分
,對角線BD平分![]() ,
,![]() 求證:
求證:![]() 是比例三角形.
是比例三角形.
![]() 如圖2,在
如圖2,在![]() 的條件下,當
的條件下,當![]() 時,求
時,求![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
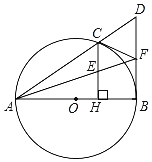
【題目】如圖,已知點C是以AB為直徑的⊙O上一點,CH⊥AB于點H,過點B作⊙O的切線交直線AC于點D,點E為CH的中點,連接AE并延長交BD于點F,連接CF.
(1)求證:CF=BF;
(2)求證:CF是⊙O的切線;
(3)若FB=FE=3,求⊙O的半徑.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】每年4月23日是世界讀書日,某校為了解學生課外閱讀情況,隨機抽取20名學生,對每人每周用于課外閱讀的平均時間(單位:min)進行調查,過程如下:
收集數據:
30 | 60 | 81 | 50 | 40 | 110 | 130 | 146 | 90 | 100 |
60 | 81 | 120 | 140 | 70 | 81 | 10 | 20 | 100 | 81 |
整理數據:
課外閱讀平均時間x(min) | 0≤x<40 | 40≤x<80 | 80≤x<120 | 120≤x<160 |
等級 | D | C | B | A |
人數 | 3 | a | 8 | b |
分析數據:
平均數 | 中位數 | 眾數 |
80 | m | n |
請根據以上提供的信息,解答下列問題:
(1)填空:a= ,b= ;m= ,n= ;
(2)已知該校學生500人,若每人每周用于課外閱讀的平均時間不少于80min為達標,請估計達標的學生數;
(3)設閱讀一本課外書的平均時間為260min,請選擇適當的統計量,估計該校學生每人一年(按52周計)平均閱讀多少本課外書?
查看答案和解析>>
科目:初中數學 來源: 題型:
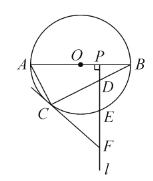
【題目】如圖,![]() 是☉
是☉![]() 的直徑,
的直徑,![]() 為☉
為☉![]() 上一點,
上一點,![]() 是半徑
是半徑![]() 上一動點(不與
上一動點(不與![]() 重合),過點
重合),過點![]() 作射線
作射線![]() ,分別交弦
,分別交弦![]() ,
,![]() 于
于![]() 兩點,過點
兩點,過點![]() 的切線交射線
的切線交射線![]() 于點
于點![]() .
.
(1)求證:![]() .
.
(2)當![]() 是
是![]() 的中點時,
的中點時,
①若![]() ,判斷以
,判斷以![]() 為頂點的四邊形是什么特殊四邊形,并說明理由;
為頂點的四邊形是什么特殊四邊形,并說明理由;
②若![]() ,且
,且![]() ,則
,則![]() _________.
_________.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com